DSC 40B – Theoretical Foundations of Data Science II
Midterm 01
Practice problems for topics on Midterm 01. See also the Sample Midterm 01 and its solutions.
Tags in this problem set:
Problem #001
Tags: time complexity
What is the time complexity of the following function in terms of \(n\)? State your answer using asymptotic notation (e.g., \(\Theta(n)\)).
def foo(n):
i = 0
while i < n**2:
i = i + 2
j = 0
while j < n:
for k in range(n):
print(i + j + k)
j = j + 10
Solution
\(\Theta(n^4)\)
Problem #002
Tags: time complexity
What is the time complexity of the following function in terms of \(n\)?
def foo(n):
for i in range(n**2):
for j in range(i):
print(i+j)
for k in range(n):
print(i+k)
for x in range(n - i):
print(x)
Solution
\(\Theta(n^4)\)
Problem #003
Tags: time complexity
What is the time complexity of the following function in terms of \(n\)?
from math import sqrt, log, ceil
def foo(n):
for i in range(ceil(n**3 - 10*n + sqrt(n))):
for j in range(ceil(log(n**2))):
print(i, j)
Solution
\(\Theta(n^3 \log n)\)
Problem #004
Tags: time complexity
What is the time complexity of the following function in terms of \(n\)?
def foo(arr):
"""`arr` is a list containing n numbers."""
for x in arr:
if x > max(arr) / 2:
print('large!')
elif x < min(arr) * 2:
print('small!')
else:
print('neither!')
Solution
\(\Theta(n^2)\)
Problem #005
Tags: best and worst case
What is the best case time complexity of the following function in terms of \(n\)?
def foo(arr):
"""`arr` is a list containing n numbers."""
previous = None
n = len(arr)
for x in arr:
if x == previous:
for i in range(n**2):
print('Equal!')
return
previous = x
Solution
\(\Theta(n)\)
Problem #006
Tags: best and worst case
What is the worst case time complexity of the function in the previous problem?
Solution
\(\Theta(n^2)\)
Problem #007
Tags: theoretical lower bounds
Suppose you are given a (possibly unsorted) array containing \(n\) elements. Each element is either zero or one. You are tasked with determining if the majority (at least half) of the array's elements are one.
What is the tight theoretical lower bound for the worst case time complexity of this problem?
Solution
\(\Theta(n)\)
Problem #008
Tags: theoretical lower bounds, sorted structure
Consider the same problem as above, except now you may assume that the array is sorted. What is the tight theoretical lower bound for the worst case time complexity of any algorithm which solves this problem?
Solution
\(\Theta(1)\)
Problem #009
Tags: expected time
What is the expected time complexity of the function below?
import random
def foo(n):
# draw a random number uniformly from 0, 1, 2, ..., 99
# in constant time
x = random.randrange(100)
for i in range(x):
for j in range(n):
print("Here!")
Solution
\(\Theta(n)\). Note that in this question, the range of \(x\) is between 0 and 99. Therefore the outer loop will run a constant number of times no matter what \(x\) is. Then we can focus on the inner loop, which runs for \(n\) times the print() operation, which is \(\Theta(n)\) time. Therefore, the expected time complexity for this piece of code is \(\Theta(n)\).
Problem #010
Tags: expected time
What is the expected time complexity of the function below?
import random
def foo(n):
# draw a number uniformly at random from 0, 1, 2, ..., n-1
# in constant time
x = random.randrange(n)
if x < 100:
for j in range(n**2):
print(j)
Solution
\(\Theta(n)\). The for loop is only executed if \(x\) is less than 100, therefore we can write the expected time as (ignoring constants \(c\)):
Problem #011
Tags: recurrence relations
State (but do not solve) the recurrence describing the run time of the following code, assuming that the input, arr, is a list of size \(n\).
def foo(arr, stop=None):
if stop is None:
stop = len(arr) - 1
if stop < 0:
return 1
last = arr[stop]
return last * foo(arr, stop - 1)
Solution
\(T(n) = T(n-1) + \Theta(1)\)
Problem #012
Tags: recurrence relations
What is the solution of the below recurrence? State your answer using asymptotic notation as a function of \(n\).
Solution
\(\Theta(n \log n)\)
Problem #013
Tags: asymptotic notation
Let \(f(n) = \displaystyle\frac{n^3 - 2n^2 + 100}{n + 10}\) True or False: \(f(n) = O(n^4)\)
Solution
True.
Problem #014
Tags: asymptotic notation
Suppose \(f(n) = \Omega(n^3)\) and \(g(n) = \Omega(n)\).
True or False: it is necessarily the case that \(f/g = \Omega(n^2)\).
Solution
False. Take \(f(n) = n^3\) and \(g(n) = n^3\). We can see from definition that \(f(n) = \Omega(n^3)\) and \(g(n) = \Omega(n)\). However,
The key takeaway for this question is, since \(g\) is on the denominator, we can make it grow arbitrarily fast, so that \(f/g\) do not meet the requirements that we want.
Problem #015
Tags: asymptotic notation
Let \(f(n) = n \cdot(\sin{n} + 1 )\). A plot of this function is shown below.
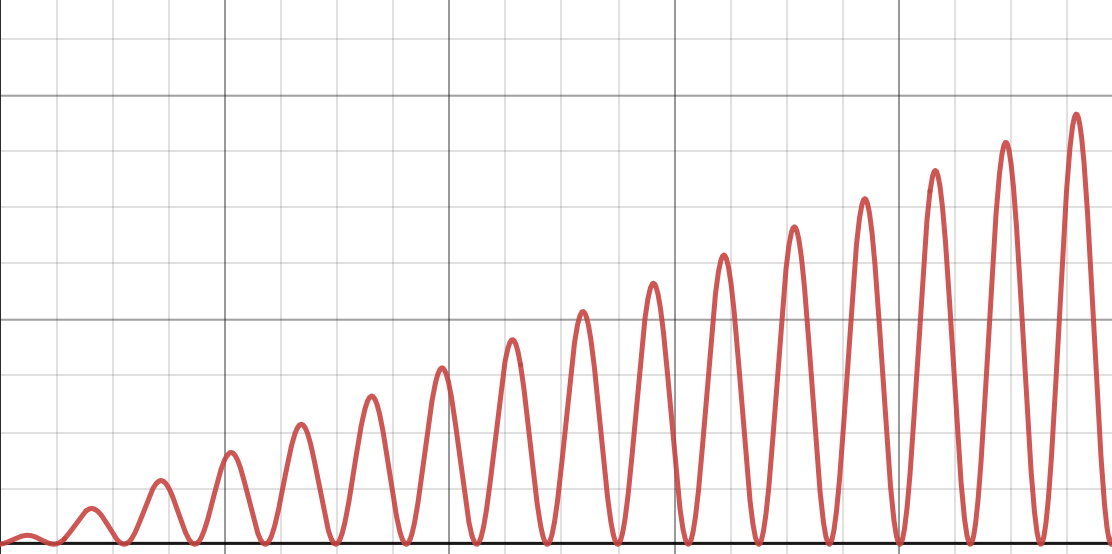
True or False: \(f(n) = \Theta(n)\).
Solution
False.
Remember that for \(f(n)\) to be \(\Theta(n)\), it has to be both upper- and lower-bounded by some positive constant times \(n\). This function is upper bounded by \(O(n)\), but it doesn't have a lower bound of \(\Omega(n)\). Therefore, it can't be \(\Theta(n)\).
In other words, there is no positive constant \(c\) and no positive number \(N\) such that \(f(n) > c n\) for all \(n > N\).
If you had to describe this function in asymptotic notation, you could say that \(f(n) = O(n)\)(and that would be a tight upper bound), but there is no lower bound, since the function keeps coming back down to zero.
Problem #016
Tags: binary search
Consider the code below, which shows binary_search as discussed in lecture, but with one additional line: a print statement.
import math
def binary_search(arr, t, start, stop):
if stop - start <= 0:
return None
middle = math.floor((start + stop)/2)
print(arr[middle]) # <---- this line is new
if arr[middle] == t:
return middle
elif arr[middle] > t:
return binary_search(arr, t, start, middle)
else:
return binary_search(arr, t, middle+1, stop)
Suppose this version of binary search is called on an array and with a target of t = 7. Which of the following statements is true?
Solution
Some of the printed values may be less than or equal to 7, and some may be greater than or equal to 7.
Problem #017
Tags: verifying recursion, binary search
Suppose we modify binary_search so that instead of using the floor operation to find the middle element of the array, we use the ceiling operation (recall that the ceiling of a real number \(x\) is the smallest integer that is \(\geq x\)). The full code is shown below for convenience:
import math
def new_binary_search(arr, start, stop, target):
if stop <= start:
return None
middle = math.ceil((start + stop) / 2)
if arr[middle] == target:
return middle
elif arr[middle] < target:
return new_binary_search(arr, middle + 1, stop, target)
else:
return new_binary_search(arr, start, middle, target)
Which of the following statements about the correctness of new_binary_search is true? You may assume that arr will be a list containing at least one number, and that the initial call to new_binary_search will be with start = 0 and stop
= len(arr) - 1.
Solution
new_binary_search may recurse infinitely
Problem #018
Tags: best and worst case, mergesort
True or False: the best case time complexity of mergesort is \(\Theta(n)\).
Solution
False.
Problem #019
Tags: mergesort
Suppose mergesort is called on an array of size \(n\). In total, how many calls to merge are made over all calls to mergesort?
Solution
\(\Theta(n)\)
Problem #020
Tags: binary search trees
Define the largest gap in a collection of numbers (also known as its range) to be greatest difference between two elements in the collection (in absolute value). For example, the largest gap in \(\{4, 9, 5, 1, 6\}\) is 8 (between 1 and 9).
Suppose a collection of \(n\) numbers is stored in a balanced binary search tree. What is the time complexity required of an efficient algorithm to calculate the largest gap in the collection? State your answer as a function of \(n\) in asymptotic notation.
Solution
\(\Theta(\log n)\). To find the largest gap, we simply need to find the minimum and the maximum in the balanced BST, which both take \(\Theta(\log{n})\) time. Therefore adding them up, the time complexity for calculating the largest gap is \(\Theta(\log{n})\).
Problem #021
Tags: time complexity
What is the time complexity of the following function?
import math
def foo(n):
for i in range(math.floor(math.sqrt(n))):
for j in range(math.floor(5*n**2 - math.sqrt(n)/1_000_000 + 100)):
print(n * n)
Solution
\(\Theta(n^2 \sqrt n)\)
Problem #022
Tags: time complexity
What is the time complexity of the following function?
def foo(arr):
"""`arr` is an array with n elements."""
x = max(arr) * min(arr)
if sum(arr) > 10:
return x
else:
return 0
Solution
\(\Theta(n)\)
Problem #023
Tags: best and worst case
The below code takes in an array of numbers and returns the index of the first maximum. What is this code's best case time complexity?
def index_of_maximum(arr):
"""`arr` is an array with n elements."""
for i, x in enumerate(arr):
if x == max(arr):
return i
Solution
\(\Theta(n)\)
Problem #024
Tags: time complexity
What is the time complexity of the following function?
def foo(n):
i = 0
while i < n:
j = 0
while j < i:
print(i + j)
j += 1
i += 5
Solution
\(\Theta(n^2)\)
Problem #025
Tags: asymptotic notation
Let \(f\) be the piecewise function defined as:
If you were to plot \(f\), the function would look like \(n^2\), but would have point discontinuities where it ``jumps'' back to 1 whenever \(n\) is a multiple of 1 million.
True or False: \(f(n) = \Theta(n^2)\).
Solution
False.
\(f(n)\)is upper bounded by \(O(n^2)\), but it doesn't have a lower bound of \(\Omega(n^2)\), which is necessary for it to be \(\Theta(n^2)\).
To see why, remember that for \(f(n)\) to be \(\Omega(n^2)\), there must be a positive constant \(c\) so that \(f(n)\) stays above \(c\cdot n^2\) for all \(n\) greater than some \(n_0\), meaning that it goes above \(c n^2\)and it stays above $c n^2$ forever, after some point.
Pick whatever positive \(c\) you'd like -- the function \(c\cdot n^2\) grows larger and larger as \(n\) increases, and eventually becomes larger than 1. But the function \(f(n)\) keeps dipping down to 1, meaning that it doesn't stay above \(c\cdot n^2\) for all \(n\) when \(n\) is large. Therefore, \(f(n)\) is not \(\Omega(n^2)\), and therefore also not \(\Theta(n^2)\).
Problem #026
Tags: asymptotic notation
Suppose \(f(n)\) is both \(O(n^2)\) and \(\Omega(n)\), and suppose \(g(n) = \Theta(n^3)\). What are the tightest possible asymptotic bounds that can be placed on \(f + g\)?
If the upper and lower bounds are the same, you may use \(\Theta\). If the upper and lower bounds are different, you should state them separately using \(O\) and \(\Omega\).
Solution
\(\Theta(n^3)\)
Problem #027
Tags: binary search trees
Suppose the numbers 41, 32, and 40 are inserted (in that order) into the below binary search tree. Draw where the new nodes will appear.
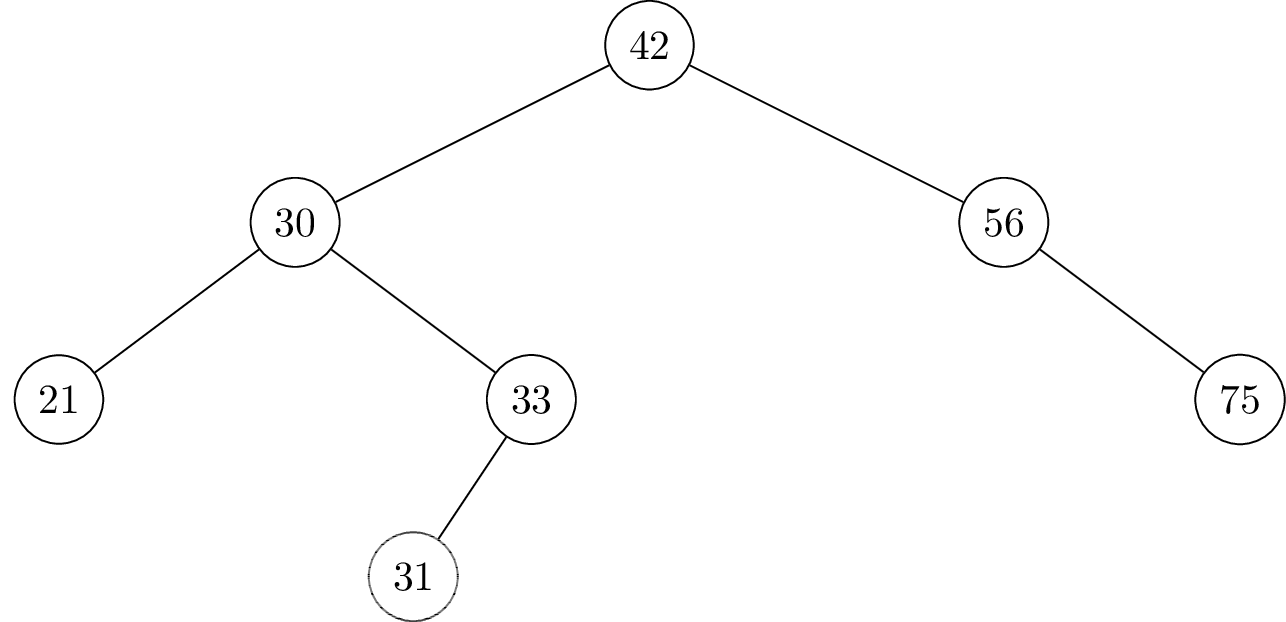
Solution
41 will be the right child of 33.
32 will be the right child of 31.
40 will be the left child of 41.
Problem #028
Tags: recurrence relations
State (but do not solve) the recurrence describing the runtime of the following function.
def foo(n):
if n < 10:
print("Hello world.")
return
for i in range(n):
print(i)
for i in range(6):
foo(n//3)
Solution
\(T(n) = 6 T(n/3) + \Theta(n)\).
Problem #029
Tags: asymptotic notation
Consider the function \(f(n) = \frac{n^8 + 2^{3 + \log n} - \sqrt n}{20 n^5 - n^2}\).
True or False: \(f(n) = O(n^{4})\).
Solution
True.
Problem #030
Tags: time complexity
What is the time complexity of the following function? State your answer using asymptotic notation (e.g., \(\Theta(n)\)).
def foo(n):
for i in range(n):
for j in range(n):
for k in range(n**2):
print(i + j + k)
Solution
\(\Theta(n^4)\)
Problem #031
Tags: asymptotic notation
Suppose \(f_1(n) = O(g_1(n))\) and \(f_2(n) = \Omega(g_2(n))\). True or False: it is necessarily the case that \(f_1 + f_2 = O(g_1(n))\).
Solution
False.
Problem #032
Tags: expected time
What is the expected time complexity of the following function?
import random
def foo(n):
for i in range(n):
# draw a number uniformly at random from 0, 1, 2, ..., n-1 in Theta(1)
x = random.randrange(n)
for j in range(x):
print(j)
Solution
\(\Theta(n^2)\). For this function, the outer loop wil execute \(n\) times no matter what, hence we only have to find what the expected time complexity for the inner loop is, then combine that together with the outer loop. For the inner loop, the expected time complexity is
Then, the expected complexity for the whole function will be
Problem #033
Tags: asymptotic notation
Let \(f\) and \(g\) be as in the previous question. What are the tightest possible asymptotic bounds that can be placed on the product, \(f \times g\)?
As before, if the upper and lower bounds are the same, you may use \(\Theta\); otherwise you should use \(O\) and \(\Omega\).
Solution
\(O(n^5)\) and \(\Omega(n^4)\)
Problem #034
Tags: binary search trees
Define the smallest gap in a collection of numbers to be the smallest difference between two distinct elements in the collection (in absolute value). For example, the smallest gap in \(\{4, 9, 1, 6\}\) is 2 (between 4 and 6).
Suppose a collection of \(n\) numbers is stored in a balanced binary search tree. What is the time complexity required for an efficient algorithm to calculate the smallest gap of the numbers in the BST? State your answer as a function of \(n\) in asymptotic notation.
Solution
\(\Theta(n)\). The smallest gap in the BST can occur between any two consecutive pairs of numbers in the BST, meaning that no matter what we need to search through the whole tree to obtain this number, taking \(\Theta(n)\) time.
Problem #035
Tags: recursion, binary search
Suppose binary_search has been called on a sorted array arr with a target t that is not necessarily in the array, and with start and stop indices start and stop, respectively (remember, our convention is that the start index is included, while the stop index is excluded from the search). Which of the following must be true? Mark all which apply. You may assume that stop - start\(\geq 1\).
Note: remember that any statement about an empty array is considered to be automatically true. Also, you cannot assume that this call to binary_search is the root call (it could be a recursive call).
Solution
The last two answers are both correct.
Problem #036
Tags: theoretical lower bounds
Suppose you are given a (possibly unsorted) array of \(n\) floating point numbers and are tasked with counting the number of elements in the array which are within ten of the array's maximum (you are not told the maximum). That is, you must count the number of elements \(x\) such that \(m - x \geq 10\), where \(m\) is the array's maximum. You may assume that the array does not contain duplicate numbers.
What is the tight theoretical lower bound for the worst case time complexity of this problem?
Solution
\(\Theta(n)\).
It takes \(\Theta(n)\) time to find the maximum. After this, we loop through and keep track of how many elements are within ten of the maximum -- this also takes \(\Theta(n)\) time.
Problem #037
Tags: expected time
What is the expected time complexity of the function below?
import random
def foo(n):
# draw a number uniformly at random from 0, 1, 2, ..., n-1 in Theta(1)
x = random.randrange(n)
if x < math.sqrt(n):
for j in range(n):
print(j)
Solution
\(\Theta(\sqrt n)\). Since the for loop only executes when \(x\) is less than \(\sqrt{n}\), the expected time complexity is
Problem #038
Tags: theoretical lower bounds
Suppose you are given a (possibly unsorted) array of \(n\) floating point numbers and are tasked with counting the number of elements in the array which are within ten of the array's maximum (you are not told the maximum). That is, you must count the number of elements \(x\) such that \(m - x \geq 10\), where \(m\) is the array's maximum. You may assume that the array does not contain duplicate numbers.
Now you may assume that the array is sorted.
This question has two parts:
First, give the tight theoretical lower bound for the worst case time complexity of any algorithm which solves this problem:
Solution
\(\Theta(\log n)\)
Second, give a short description of an optimal algorithm. Your description does not need to be exact or very long (3 to 4 sentences will do). You do not need to provide pseudocode, but you can if you wish.
Solution
The maximum \(m\) can be found in \(\Theta(1)\) time -- it is the last element of the array. Use binary search (\(\Theta(\log n)\) time) to look for \(m - 10\), but modify the code so that the last-checked index is returned if \(m - 10\) is not found (everything to the right of that index is at least \(m - 10\)). Subtract this index from \(n\) to find the number of elements within 10 of the maximum.
Problem #039
Tags: time complexity
What is the time complexity of the following function? State your answer using asymptotic notation (e.g., \(\Theta(n)\)).
def foo(n):
for i in range(n):
for j in range(n**2):
for k in range(n):
print(i + j + k)
Solution
\(\Theta(n^4)\)
Problem #040
Tags: best and worst case
The below code takes in an array of numbers and returns the index of the first maximum.
def foo(arr):
"""`arr` is an array with n elements."""
for i, x in enumerate(arr):
if x == max(arr):
return i
What is the worst case time complexity of the function?
Solution
\(\Theta(n^2)\)
Problem #041
Tags: recursion, binary search
Suppose binary_search is called on a sorted array of size \(n\). In total, how many recursive calls to binary_search are made in the worst case?
Solution
\(\Theta(\log n)\)
Problem #042
Tags: verifying recursion
Consider the code below which claims to compute the maximum of the input array. Adopt the convention that the maximum of an empty array is \(-\infty\).
import math
def maximum(arr, start=0, stop=None):
"""Find the maximum of arr[start:stop]."""
if stop is None:
stop = len(arr)
if stop - start == 0:
return -float('inf')
middle = math.floor((start + stop) / 2)
left = maximum(arr, start, middle)
right = maximum(arr, middle, stop)
if left > right:
return left
else:
return right
Will this code always return the correct answer (the maximum)? If yes, simply say so. If no, describe what might happen (recurse infinitely, return the wrong answer, raise an index error, etc.).
Solution
This code will recurse infinitely when called on an array with a single element.
Problem #043
Tags: asymptotic notation
Consider the function \(f(n) = \frac{n^8 + 2^{3 + \log n} - \sqrt n}{20 n^5 - n^2}\).
True or False: \(f(n) = \Omega(n^2)\).
Solution
True.
Problem #044
Tags: recurrence relations
Solve the below recurrence, stating the solution in asymptotic notation. Show your work.
Solution
\(\Theta(n)\).
We'll unroll several times:
The pattern seems to be that on the \(k\)th unroll:
The base case is reached when \(k = \log_4 n\). Plugging this back in, we find:
If you reached this point, you got most of the credit. If you're unsure of what to do with \(2^{\log_4 n}\), there are a couple of ways foward.
The first (and easiest) way is to realize that \(2^{\log_4 n}\) is smaller than \(2^{\log_2 n} = n\), so \(2^{\log_4 n} = O(n)\). Similarly, we've seen the summation of \(1 + 1/2 + 1/4 + \ldots\) several times -- this is a geometric sum, and converges to 2 when there are infinitely many terms. There are a finite number of terms here, so the sum is \(< 2\). Altogether, we have:
The second approach is to remember log properties to simplify \(2^{\log_4 n}\) to \(\sqrt{n}\). This can be seen by using the ``change of base'' formula:
In this case:
And therefore \(2^{\log_4 n} = 2^{(\log_2 n) / 2} = \left(2^{\log_2 n}\right)^{1/2} = n^{1/2} = \sqrt n\). This shows that the first term in the recurrence is \(\Theta(\sqrt n)\). The second term is still \(\Theta(n)\), so the solution is \(\Theta(n)\).
Problem #045
Tags: asymptotic notation
Suppose Algorithm A takes \(\Theta(n^2)\) time, while Algorithm B takes \(\Theta(2^n)\) time. True or False: there could exist an input on which Algorithm \(B\) takes less time than Algorithm A.
Solution
True.
Problem #046
Tags: asymptotic notation
Let
True or False: \(f(n) = \Theta(n^2)\).
Solution
False.
Problem #047
Tags: binary search
Consider the problem of searching for an element t in a sorted array, with the added requirement that if t is in the array multiple times, we return the index of the first occurrence. For example, if arr = [3, 4, 4, 4, 5, 8], and t = 4, the code should return 1, since the first 4 is at index one.
binary_search as implemented in lecture may not necessarily return the index of the first occurrence of t, but it can be modified so that it does.
Fill in the blanks below so that the function returns the index of the first occurence of t. Hint: last_seen should keep track of the index of the last known occurrence of t.
import math
def mbs(arr, t, start, stop, last_seen=None):
if start - stop <= 0:
return last_seen
middle = math.floor((stop - start) / 2)
if arr[middle] == t:
# _________ <-- fill this in
elif arr[middle] < t:
# _________ <-- fill this in
else:
# _________ <-- fill this in
Solution
Here is how the blanks should be filled in:
if arr[middle] == t:
return mbs(arr, t, start, middle, middle)
elif arr[middle] < t:
return mbs(arr, t, middle + 1, stop, last_seen)
else:
return mbs(arr, t, start, middle, last_seen)
If we see arr[middle] == t, we know that this is either the first occurrence of t in the array, or the first occurrence of t in the left half of the array. Therefore, we make a recursive call to mbs on the left half of the array, keeping track of middle as the index of the leftmost occurrence of t we have seen so far (this is done by passing it as the value to last_seen).
The other recursive calls are the same as in the original binary_search function, except that we pass last_seen as an argument to the recursive calls. This is because we want to keep track of the leftmost occurrence of t we have seen so far.
Eventually, we will reach a point where start - stop <= 0. At this point, we return last_seen, which is the index of the leftmost occurrence of t we have seen so far. This will necessarily be the leftmost occurrence of t in the array.
Problem #048
Tags: quickselect
True or False: quickselect requires the input array to be sorted in order to function correctly.
Solution
False.
Problem #049
Tags: time complexity
Express the time complexity of the following code using asymptotic notation in as simplest terms possible.
def foo(n):
for i in range(200, n):
for j in range(i, 2*i + n**2):
print(i + j)
Solution
\(\Theta(n^3)\)
Problem #050
Tags: time complexity
Express the time complexity of the following code using asymptotic notation in as simplest terms possible.
import math
def foo(arr):
"""`arr` is an array with n elements."""
n = len(arr)
ix = 1
s = 0
while ix < n:
s = s + arr[ix]
ix = ix * 5 + 2
return s
Solution
\(\Theta(\log n)\)
Problem #051
Tags: best and worst case
The code below takes in an array of \(n\) numbers and checks whether there is a pair of numbers in the array which, when added together, equal the maximum element of the array.
What is the best case time complexity of this code as a function of \(n\)? State your answer using asymptotic notation.
def exists_pair_summing_to_max(arr):
n = len(arr)
maximum = max(arr)
for i in range(n):
for j in range(i + 1, n):
if arr[i] + arr[j] == maximum:
return True
return False
Solution
\(\Theta(n)\)
Problem #052
Tags: time complexity
Express the time complexity of the following code using asymptotic notation in as simplest terms possible.
def foo(n):
for i in range(n):
for j in range(i):
for k in range(n):
print(i + j + k)
Solution
\(\Theta(n^3)\)
Problem #053
Tags: binary search
Consider the version of binary search shown below:
import math
def binary_search(arr, t, start, stop):
"""
Searches arr[start:stop] for t.
Assumes arr is sorted.
"""
if stop - start <= 0:
return None
middle = math.floor((start + stop)/2)
if arr[middle] == t:
return middle
elif arr[middle] > t:
return binary_search(arr, t, start, middle)
else:
return binary_search(arr, t, middle+1, stop)
True or false: if the target element t occurs multiple times in the array, binary_search is guaranteed to return the first occurrence.
You may assume that arr is sorted and that binary_search(arr, t, 0, len(arr)) is called.
Solution
False.
Problem #054
Tags: asymptotic notation
Consider the function \(f(n) = n \times(\sin(n) + 1)\). A plot of this function is shown below:
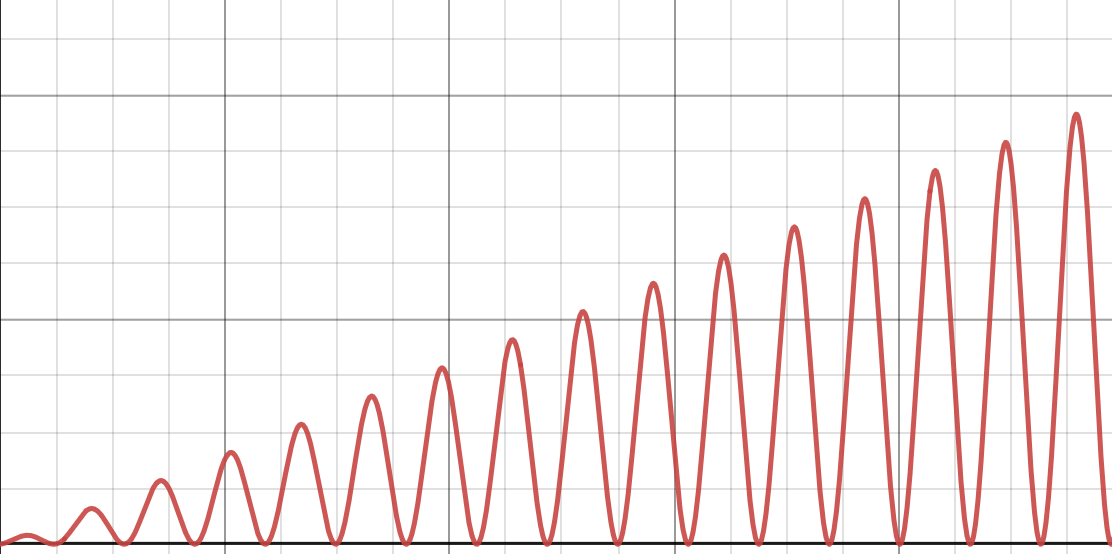
True or False: this function is \(O(1 + \sin n)\).
Solution
False.
\(f(n)\) grows arbitrarily large, while \(\sin n + 1\) is bounded above by 2.
More formally, there is no constant \(c\) such that \(c (1 + \sin n)\) upper bounds \(f(n)\) for all large \(n\).
Problem #055
Tags: binary search trees
Suppose the numbers 41, 32, and 33 are inserted (in that order) into the below binary search tree. Draw where the new nodes will appear.
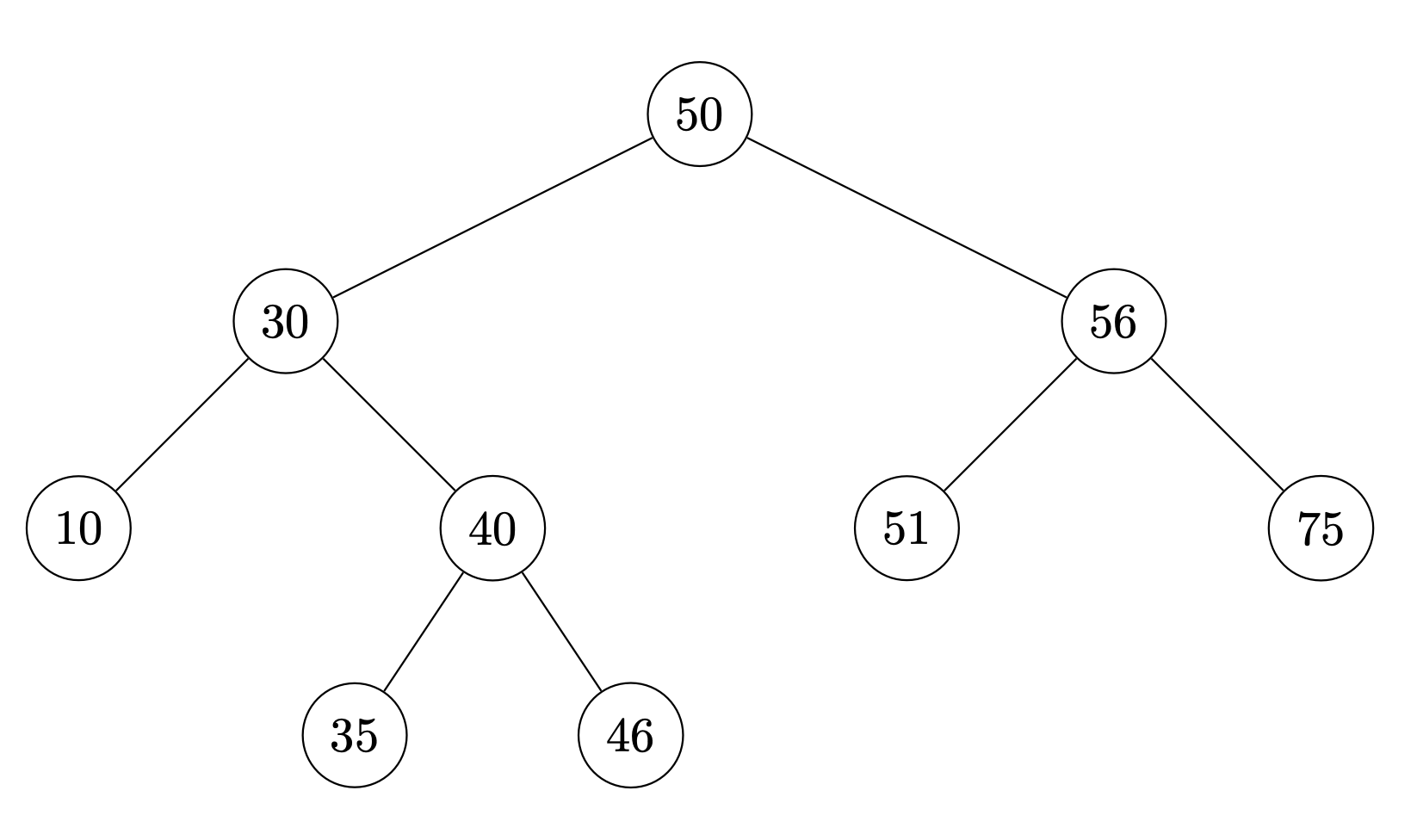
Solution
41 will become the left child of 46.
32 will become the left child of 35.
33 will become the right child of 32.
Problem #056
Tags: recurrence relations
State (but do not solve) the recurrence describing the runtime of the following function.
def foo(n):
if n < 1:
return 0
for i in range(n**2):
print("here")
foo(n/2)
Solution
\( T(n) = \begin{cases} \Theta(1), & n = 1\\ T(n/2) + \Theta(n^2)% , & n > 1 \end{cases}\)
Problem #057
Tags: asymptotic notation
Suppose \(f_1(n)\) is \(O(n^2)\) and \(\Omega(n)\). Also suppose that \(f_2(n) = \Theta(n^2)\).
Consider the function \(g(n) = f_2(n) / f_1(n)\). True or false: it must be the case that \(g(n) = \Omega(n)\).
Solution
False.
Problem #058
Tags: asymptotic notation
Suppose \(f_1(n) = \Omega(g_1(n))\) and \(f_2 = \Omega(g_2(n))\). Define \(f(n) = \min\{ f_1(n), f_2(n) \}\) and \(g(n) = \min\{ g_1(n), g_2(n)\}\).
True or false: it is necessarily the case that \(f(n) = \Omega(g(n))\).
Solution
True.
Problem #059
Tags: expected time
What is the expected time complexity of the following function? State your answer using asymptotic notation.
import random
def foo(n):
x = random.randrange(n)
if x < 8:
for j in range(n**3):
print(j)
else:
for j in range(n):
print(j)
Solution
\(\Theta(n^2)\). The expected time complexity for this function is
Problem #060
Tags: asymptotic notation
Consider again the function \(f(n) = n \times( \sin(n) + 1)\) from the previous problem.
True or False: \(f(n) = O(n^3)\).
Solution
True.
Problem #061
Tags: binary search trees
Define the largest gap in a collection of numbers to be the largest difference between two distinct elements in the collection (in absolute value). For example, the largest gap in \(\{4, 9, 1, 6\}\) is 8 (between 1 and 9).
Suppose a collection of \(n\) numbers is stored in a balanced binary search tree. What is the time complexity required for an efficient algorithm to calculate the largest gap of the numbers in the BST? State your answer as a function of \(n\) in asymptotic notation.
Solution
\(\Theta(\log n)\). With the same reasoning as Problem 20, we only require the largest and smallest number in the BST in order to find the largest gap (just subtract the smallest from the largest number), therefore the time complexity of this operation in a balanced BST will be \(\Theta(\log{n})\).
Problem #062
Tags: loop invariants, binary search
Consider the iterative implementation of binary search shown below:
import math
def iterative_binary_search(arr, target):
start = 0
stop = len(arr)
while (stop - start) > 0:
print(arr[start])
middle = math.floor((start + stop) / 2)
if arr[middle] == target:
return middle
elif arr[middle] > target:
stop = middle
else:
start = middle + 1
return None
Which of the following loop invariants is true, assuming that arr is sorted and non-empty, and target is not in the array? Select all that apply.
Solution
The first option is correct.
Problem #063
Tags: theoretical lower bounds
Consider again the problem of determining whether there exists a pair of numbers in an array which, when added together, equal the maximum number in the array. Additionally, assume that the array is sorted.
True or False: \(\Theta(n)\) is a tight theoretical lower bound for this problem.
Solution
True.
Any algorithm must take \(\Omega(n)\) time in the worst case, since in the worst case all elements of the array must be read.
This is tight because there is an algorithm that will compute the answer in worst-case \(\Theta(n)\) time. Namely, this is an instance of the ``movie problem'' from lecture, where instead of finding two numbers which add to an arbitrary target, we're looking for a specific target: the maximum. We saw an algorithm that solved the movie problem in \(\Theta(n)\) time, where \(n\) was the number of movies. Since the maximum is computed in \(\Theta(1)\) time for a sorted array, we can use the same algorithm to solve this in \(\Theta(n)\) time as well.
Problem #064
Tags: expected time
What is the expected time complexity of the function below? State your answer using asymptotic notation.
You may assume that math.sqrt and math.log take \(\Theta(1)\) time. math.log computes the natural log.
import random
import math
def foo(n):
# draw a number uniformly at random from 0, 1, 2, ..., n-1 in Theta(1)
x = random.randrange(n)
if x < math.log(n):
for j in range(n**2):
print(j)
elif x < math.sqrt(n):
print('Ok!')
else:
for i in range(n):
print(i)
Solution
\(\Theta(n \log n)\) There are three cases: Case 1) \(x < \log n\); Case 2) \(\log n \geq x < \sqrt n\); and Case 3) \(x \geq\sqrt{n}\).
The probability of Case 1 is \(\log n / n\). The time taken in case 1 is \(\Theta(n^2)\).
The probability of Case 2 is
The time taken in this case is \(\Theta(1)\).
The probability of Case 3 is 1 minus the probability of the sum of the other two cases, which will simply be \(\Theta(1)\):
Therefore, the expected time is:
Problem #065
Tags: theoretical lower bounds, sorted structure
Suppose \(a\) and \(b\) are two numbers, with \(a \leq b\). Consider the problem of counting the number of elements in an array which are between \(a\) and \(b\); that is, the number of elements \(x\) such that \(a \leq x \leq b\). You may assume for simplicity that both \(a\) and \(b\) are in the array, and there are no duplicates.
Part 1)
What is a tight theoretical lower bound for this problem, assuming that the array is unsorted? State your answer in asymptotic notation as a function of the number of elements in the array, \(n\).
Solution
\(\Theta(n)\).
Since the array is in arbitrary order, we have to at least read all of the elements, taking \(\Omega(n)\) time. This is a tight lower bound, because we can count the number of elements between \(a\) and \(b\) by looping through and checking whether each element is in \([a, b]\) in linear time.
Part 2)
What is a tight theoretical lower bound for this problem, assuming that the array is sorted? State your answer in asymptotic notation as a function of the number of elements in the array, \(n\).
Solution
\(\Theta(\log n)\).
We can do this in worst-case \(\Theta(\log n)\) time with binary search: find the index of \(a\) in worst-case \(\Theta(\log n)\) time; find the index of \(b\) in worst-case \(\Theta(\log n)\) time; and subtract the two indices (and add one) to get the total number of elements between \(a\) and \(b\), inclusive.
There cannot be an algorithm that is better than \(\Theta(\log n)\) in the worst case, so this is a tight lower bound. To see why, recognize that we can solve the query problem (determine True/False if a target \(t\) is in a sorted array) with any algorithm that solves this problem by setting \(a = b = t\). If an algorithm solves this problem in faster than \(\Theta(\log n)\), it will also solve the query problem in faster than \(\Theta(\log n)\), but we saw in class that the query problem has a theoretical lower bound of \(\Theta(\log n)\), so such an algorithm cannot exist.
Problem #066
Tags: time complexity
Express the time complexity of the following code using asymptotic notation in as simplest terms possible.
def foo(n):
for i in range(n**3):
for j in range(n):
print(i + j)
for j in range(n**2):
print(i + j)
Solution
\(\Theta(n^5)\)
Problem #067
Tags: best and worst case
What is the worst case time complexity of the function in the last problem? State your answer using asymptotic notation.
Solution
\(\Theta(n^2)\)
Problem #068
Tags: recurrence relations, mergesort
Consider the modification of mergesort shown below, where one of the recursive calls has been replaced by an in-place version of selection_sort. Recall that selection_sort takes \(\Theta(n^2)\) time.
def kinda_mergesort(arr):
"""Sort array in-place."""
if len(arr) > 1:
middle = math.floor(len(arr) / 2)
left = arr[:middle]
right = arr[middle:]
mergesort(left)
selection_sort(right)
merge(left, right, arr)
What is the time complexity of kinda_mergesort?
Solution
\(\Theta(n^2)\)
Problem #069
Tags: recursion, verifying recursion
Consider the code below which claims to compute the most common element in the array, returning a pair: the element along with the number of times it appears.
import math
def most_common(arr, start, stop):
"""Attempts to compute the most common element in arr[start:stop]."""
if stop - start == 1:
return (arr[start], 1)
middle = math.floor((start + stop) / 2)
left_value, left_count = most_common(arr, start, middle)
right_value, right_count = most_common(arr, middle, stop)
if left_count > right_count:
return (left_value, left_count)
else:
return (right_value, right_count)
You may assume that the function is always called on a non-empty array, and with start = 0 and stop = len(arr). Will this code always return the correct answer (the most common element)?
Solution
No: it will run without error, but the element returned may not be the most common element in the array.
It is not true in general that the most common element in the array is the most common in the left or the right. As a simple example, take: [1,1,1,0,0,2,2,2,0,0]. 1 is the most common in the left half, and 2 is the most common in the right half, but 0 is the most common overall.
So even if we assume that most_common(arr, start, middle) finds the most common element in left half of the array, and most_common(arr, middle, stop) finds the most common element in the right of the array, it is not necessarily the case that the most common between them is the overall most common in the array.
You can also quickly see that the code cannot be correct because nowhere is a count greater than one ever returned.
Problem #070
Tags: asymptotic notation
Suppose \(f_1(n)\) is \(O(n^2)\) and \(\Omega(n)\). Also suppose that \(f_2(n) = \Theta(n^2)\).
Consider the function \(f(n) = f_1(n) + f_2(n)\). True or false: it must be the case that \(f(n) = \Theta(n^2)\).
Solution
True.
Problem #071
Tags: recurrence relations
Solve the below recurrence, stating the solution in asymptotic notation. Show your work.
Solution
\(\Theta(n)\).
Unrolling several times, we find:
On the \(k\)th unroll, we'll get:
It will take \(\log_2 n\) unrolls to each the base case. Substituting this for \(k\), we get:
Problem #072
Tags: time complexity
Suppose bar and baz are two functions. Suppose bar's time complexity is \(\Theta(n^3)\), while baz's time complexity is \(\Theta(n^2)\).
Suppose foo is defined as below:
def foo(n):
if n < 1_000:
bar(n)
else:
baz(n)
What is the asymptotic time complexity of foo?
Solution
\(\Theta(n^2)\)
Problem #073
Tags: asymptotic notation
Let
Write \(f\) in asymptotic notation in as simplest terms possible.
Solution
\(f(n) = \Theta(n^2)\)
Problem #074
Tags: loop invariants, binary search
Consider iterative_binary_search below and note the print statement in the while-loop:
import math
def iterative_binary_search(arr, target):
start = 0
stop = len(arr)
while (stop - start) > 0:
print(arr[start])
middle = math.floor((start + stop) / 2)
if arr[middle] == target:
return middle
elif arr[middle] > target:
stop = middle
else:
start = middle + 1
return None
Suppose iterative_binary_search is run on the array:
[-202, -201, -200, -50, -20, -10, -4, -3, 0, 1, 3, 5, 6, 7, 9, 10, 12, 15, 22]
with target 11.
What will be the last value of arr[start] printed?
Solution
10
Problem #075
Tags: loop invariants, quickselect
Recall the partition operation from quickselect. Which of the following arrays could have been partitioned at least once? Select all that apply.
Solution
The second, third, and last all should be selected.
Problem #076
Tags: time complexity
The function below counts how many elements What is the time complexity of the following function in terms of \(n\)? Remember to state your answer in the simplest terms possible.
from math import sqrt, log, ceil
def foo(n):
for i in range(ceil(n**3 - 10*n + sqrt(n))):
for j in range(ceil(log(n**2))):
print(i, j)
Solution
\(\Theta(n^3 \log n)\)
Problem #077
Tags: time complexity
What is the time complexity of the following function in terms of \(n\)?
def foo(arr):
"""`arr` is a list containing n numbers."""
for x in arr:
n = len(arr)
if x > sum(arr) / n:
print('large!')
elif x < sum(arr) / n:
print('small!')
else:
print('neither!')
Solution
\(\Theta(n^2)\)
Problem #078
Tags: best and worst case
What is the best case time complexity of the following function in terms of \(n\)?
def foo(arr):
"""`arr` is a list containing n numbers."""
previous = None
n = len(arr)
for x in arr:
if x == previous:
for i in range(n**2):
print('Equal!')
return
previous = x
Solution
\(\Theta(n)\)
Problem #079
Tags: time complexity
What is the time complexity of the following function in terms of \(n\)?
import math
def foo(n):
for i in range(math.floor(math.sqrt(n))):
for j in range(i):
print(i + j)
Solution
\(\Theta(n)\)
Problem #080
Tags: binary search trees
Suppose a collection of \(n\) numbers is stored in a balanced binary search tree. What is the time complexity required of an efficient algorithm to calculate the mean of the collection? State your answer as a function of \(n\) in asymptotic notation.
Solution
\(\Theta(n)\). Without knowing any information on the numbers, the best we can do to compute the mean is to add all numbers in the BST divided by the total number of nodes in the BST. To do this, we will have to traverse the entire BST no matter what (via some traversal algorithm), which takes \(\Theta(n)\) time. (Note that the word \(\textbf{balanced}\) does not help in this question!!!)
Problem #081
Consider the code for mergesort and merge where a new print-statement has been added to merge:
def mergesort(arr):
"""Sort array in-place."""
if len(arr) > 1:
middle = math.floor(len(arr) / 2)
left = arr[:middle]
right = arr[middle:]
mergesort(left)
mergesort(right)
merge(left, right, arr)
def merge(left, right, out):
"""Merge sorted arrays, store in out."""
left.append(float('inf'))
right.append(float('inf'))
left_ix = 0
right_ix = 0
for ix in range(len(out)):
print("Here!") # <---- the newly-added line
if left[left_ix] < right[right_ix]:
out[ix] = left[left_ix]
left_ix += 1
else:
out[ix] = right[right_ix]
right_ix += 1
Suppose mergesort is called on an array of size \(n\). In total, how many times will "Here!" be printed?
Solution
\(\Theta(n \log n)\)
Problem #082
Tags: recurrence relations
Solve the recurrence below, stating the solution in asymptotic notation. Show your work.
Solution
\(\Theta(n)\)
Problem #083
Tags: recursion, binary search, verifying recursion
Suppose we modify binary_search so that instead of using the floor operation to find the middle element of the array, we use the ceiling operation (recall that the ceiling of a real number \(x\) is the smallest integer that is \(\geq x\)). The full code is shown below for convenience:
import math
def new_binary_search(arr, start, stop, target):
if stop <= start:
return None
middle = math.ceil((start + stop) / 2)
if arr[middle] == target:
return middle
elif arr[middle] < target:
return new_binary_search(arr, middle + 1, stop, target)
else:
return new_binary_search(arr, start, middle, target)
You may assume that arr will be a sorted list containing at least one number, and that the initial call to new_binary_search will be with start = 0 and stop = len(arr).
Part 1)
True or False: there are input arrays on which new_binary_search will recurse infinitely.
Solution
True.
Part 2)
True or False: there are input arrays on which new_binary_search will raise an IndexError because it attempts to access an element of the array which does not exist.
Solution
True.
Problem #084
Tags: best and worst case
True or False: the best case time complexity of mergesort is \(\Theta(n)\).
Solution
False.
Problem #085
Tags: recurrence relations
State (but do not solve) the recurrence describing the run time of the following code, assuming that the input, arr, is a list of size \(n\).
def foo(arr, stop=None):
if stop is None:
stop = len(arr) - 1
if stop < 0:
return 1
last = arr[stop]
return last * foo(arr, stop - 1)
Solution
\(T(n) = T(n-1) + \Theta(1)\)
Problem #086
Tags: quickselect
True or False: in order to guarantee that its output is correct, quickselect must be called on a sorted list.
Solution
False.
Problem #087
Tags: theoretical lower bounds
Consider the following problem: given a (possibly unsorted) list of size \(n\) containing only ones and zeros, determine if the number of ones is equal to the number of zeros.
Part 1)
What is a tight theoretical lower bound for this problem? State your answer as a function of \(n\) using asymptotic notation.
Solution
\(\Theta(n)\)
Part 2)
Now assume that the input array is guaranteed to have the following structure: there will be \(a\) ones, followed by \(b\) zeros, followed again by \(a\) ones. An example of such an array is: [1, 1, 0, 0, 0, 1, 1]. In this example, \(a = 2\) and \(b = 3\).
Consider the same problem as before: that is, given an array satisfying the above assumption, determine if the number of ones in the array is equal to the number of zeros. Of course, \(a\) and \(b\) are not known ahead of time.
What is a tight theoretical lower bound for this problem?
Solution
\(\Theta(1)\) Let \(n\) be the length of the array. Assume that \(n\) is even (if it is odd, we can immediately say that there are not an equal number of ones and zeros). In fact, we can assume that \(n\) is divisible by four, since \(n = a + b + a = 2a + b\), which must equal \(4a\) if there are an equal number of ones and zeros.
For there to be an equal number of ones as zeros, the middle \(n/2\) elements must be zero, while the first \(n/4\) and last \(n/4\) must be ones. If that is the case, then the last one in the first group of ones will occur at index \(n / 4 - 1\), and the first zero will occur at \(n / 4 \) A constant-time algorithm is to check the element at index \(n/4 - 1\) and verify that it is a one. Then we check the element at index \(n/4 \) and check that it is a zero.
Consider, for example, this array with \(n = 10\):
Then \(n / 10 = 10 / 4 = 2.5 = 2\). Therefore, we check the elements at index 1 and 2 in constant time and find them to both be one, which tells us that this array does not have an equal number of zeros and ones.
Now consider the array below:
Since \(n = 8\), we again check the elements at index 1 and 2. We find 1 and 0, which tells us that the array does have an equal number of zeros and ones, as expected.
Problem #088
Tags: expected time
What is the expected time complexity of the function below?
You may assume that math.sqrt takes \(\Theta(1)\) time.
import random
import math
def foo(n):
# draw a number uniformly at random from 0, 1, 2, ..., n-1 in Theta(1)
x = random.randrange(n)
if x < math.sqrt(n):
for j in range(n):
print(j)
elif x < n//2:
print('Ok!')
else:
for i in range(n**2):
print(i)
Solution
\(\Theta(n^2)\). The expected time complexity for this function is
Problem #089
Tags: expected time
What is the expected time complexity of the function below?
import random
def foo(n):
# draw a random number uniformly from 0, 1, 2, ..., n-1
# in constant time
x = random.randrange(n)
for i in range(x):
for j in range(n):
print("Here!")
Solution
\(\Theta(n^2)\). The inner loop is not random, and the time complexity of it is always \(\Theta(n)\). Therefore the expected time complexity of this function will be (using the arithmetic sequence sum formula)
Problem #090
Tags: time complexity
What is the time complexity of the following function in terms of \(n\)? State your answer using asymptotic notation (e.g., \(\Theta(n)\)).
def foo(n):
for i in range(n**3):
for j in range(n):
print(i + j)
for k in range(n):
for l in range(n**2):
print(k * l)
Solution
\(\Theta(n^4)\)
Problem #091
Tags: asymptotic notation
Suppose \(f_1(n) = O(g_1(n))\) and \(f_2 = O(g_2(n))\). Define \(f(n) = \min\{ f_1(n), f_2(n) \}\) and \(g(n) = \min\{ g_1(n), g_2(n) \}\). True or false, it is necessarily the case that \(f(n) = O(g(n))\).
Solution
True.
Problem #092
Tags: time complexity
Suppose bar and baz are two functions. Suppose bar's asymptotic time complexity is \(\Theta(n^4)\), while baz's is \(\Theta(n)\).
Suppose foo is defined as below:
def foo(n):
if n < 1_000_000:
bar(n)
else:
baz(n)
What is the asymptotic time complexity of foo?
Solution
\(\Theta(n)\) If you were to plot the function \(T(n)\) that gives the time taken by foo as a function of \(n\), you'd see something like the below:
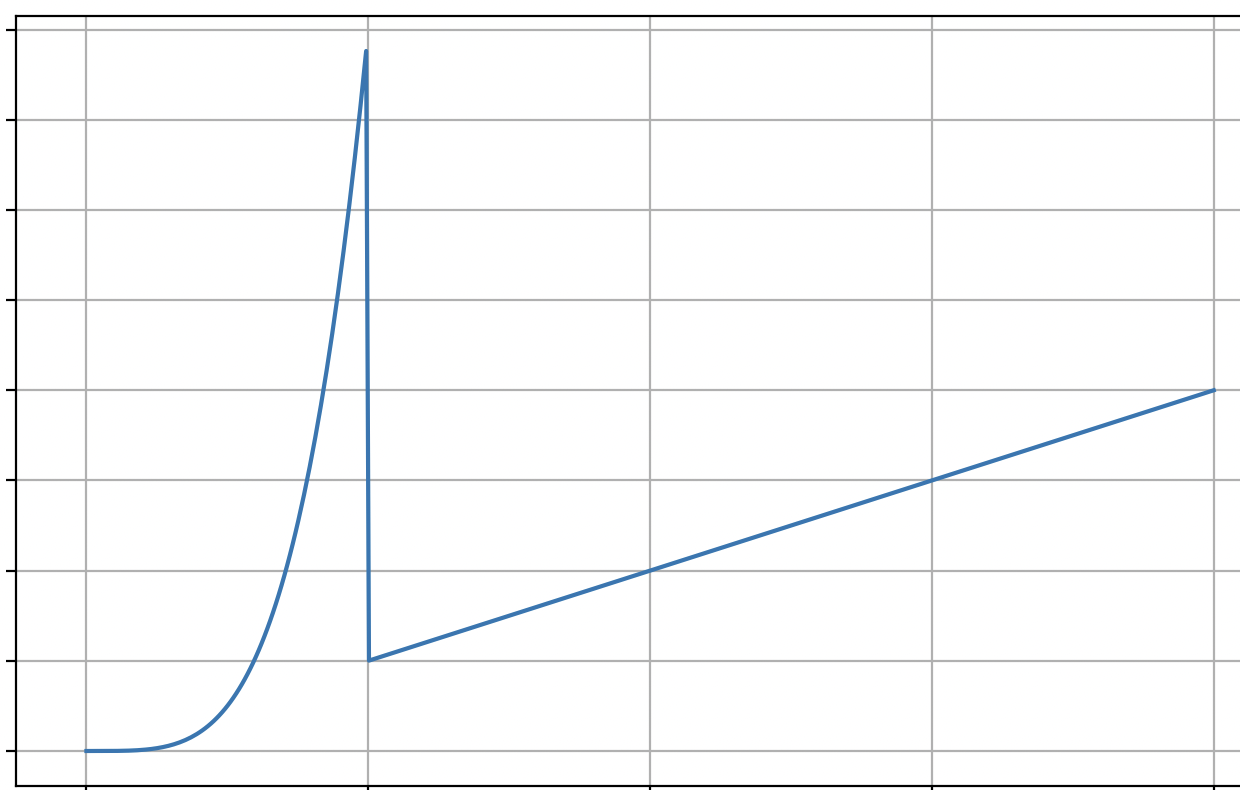
This function starts off looking like \(n^4\), but at \(n = 1_000_000\), it "switches" to looking like \(n\).
Since asymptotic time complexity is concerned with the behavior of the function as \(n\) gets large, we can ignore the part where \(n\) is "small" (in this case, less than \(1{,}000{,}000\)). So, asymptotically, this function is \(\Theta(n)\).
Problem #093
Tags: asymptotic notation
Suppose \(f(n) = \Omega(n^3)\) and \(g(n) = \Omega(n)\).
True or False: it is necessarily the case that \(f/g = \Omega(n^2)\).
Solution
False.
Problem #094
Tags: time complexity
Suppose bar and baz are two functions. Suppose bar's time complexity is \(\Theta(n^2)\), while baz's time complexity is \(\Theta(n)\).
Suppose foo is defined as below:
def foo(n):
# will be True if n is even, False otherwise
is_even = (n % 2) == 0
if is_even:
bar(n)
else:
baz(n)
Let \(T(n)\) be the time taken by foo on an input of sized \(n\). True or False: \(T(n) = \Theta(n^2)\).
Solution
False.
This function is not \(\Theta(n^2)\). For that matter, it is also not \(\Theta(n)\). It is\(O(n^2)\) and \(\Omega(n)\), though.
This function cannot be \(\Theta(n^2)\) because there are no positive constants \(c, n_0\) such that \(T(n) > c n^2\) for all \(n > n_0\). You can see this by imagining the plot of the time taken by foo as a function of \(n\). It "oscillates" between something that grows like \(n\) and something that grows like \(n^2\). If you tried to lower bound it with \(cn^2\), \(T(n)\) would eventually dip below \(cn^2\), since \(cn^2\) grows faster than \(n\).
Problem #165
Tags: time complexity
What is the time complexity of the following function? State your answer as a function of \(n\) using asymptotic notation in the simplest form possible. (e.g., \(\Theta(n)\))
def boo(n):
for i in range(200, n):
for j in range(i, i * n):
print(i + j)
boo(202)
Solution
If you count the number of times the inner loop body executes, you'll get something like \(n + 2n + 3n + \ldots + n\times n\). Factoring out the \(n\) and using the formula for the sum of the first \(n\) integers, we get \(n (1 + 2 + 3 + \ldots + n) = n \Theta(n^2) = \Theta(n^3)\).
Problem #166
Tags: time complexity
What is the time complexity of the following function? State your answer as a function of \(n\) using asymptotic notation in the simplest form possible. (e.g., \(\Theta(n)\))
import math
def boo(n):
i = n
while i > 1:
i = i / 2
for j in range(1_000_000):
print(i + j)
boo(100)
Problem #167
Tags: best and worst case
The code below takes in two lists, each containing \(n\) integers, and determines if the any number in the second list appears at least \(n/2\) times in the first list.
def boo(first_list, second_list):
"""first_list and second_list are both of size n"""
n = len(first_list)
for x in second_list:
count = 0
for y in first_list:
if x == y:
count += 1
if count >= n // 2:
return True
return False
print(boo([1, 6, 6, 4, 6], [6, 7, 8, 9, 10]))
Part 1)
What is the best case time complexity of this code as a function of \(n\)? State your answer using asymptotic notation.
Part 2)
What is the worst case time complexity of this code as a function of \(n\)? State your answer using asymptotic notation.
Solution
The best case is when the first element of the second list appears at least \(n/2\) times in the first list. In this case, the code will return True after iterating \(n/2\) times through the inner loop, taking \(\Theta(n)\) time total.
In the worst case, there is no element in the second list that appears \(n/2\) times in the first. We make all \(n\) iterations of the outer loop, and during each of the outer iterations, make \(n\) iterations of the inner loop, for a total of \(\Theta(n^2)\) time.
Problem #168
Tags: time complexity
What is the time complexity of the following function? State your answer as a function of \(n\) using asymptotic notation in the simplest form possible. (e.g., \(\Theta(n)\))
import math
def boo(n):
for i in range(n):
for j in range(n):
print(i + j)
for i in range(math.floor(math.sqrt(n))):
for j in range(math.log2(i), i * math.floor(math.log2(i + 10))):
print(i + j)
Solution
The second loop looks complicated to analyze, but we can effectively ignore it. This is because the most i can ever be is \(\sqrt
n\), and so an upper bound for the number of iterations made by the second loop is \(O(\sqrt n \log n)\). Since the first loop takes \(\Theta(n^2)\), it will dominate the time complexity, and we do not need to worry about the time taken by the second loop.
Problem #169
Tags: recursion
Professor Billy claims to have invented a new sorting algorithm: mediansort. The algorithm supposedly works by finding a median number, swapping it into the middle of the list, and recursing on the left half and the right half. Professor Billy's code is written below:
import math
def mediansort(arr, start, stop):
"""Claims to sort the array, in-place."""
if stop - start <= 1:
return
# finds the index of the median of arr[start:stop]
median_ix = find_median(arr, start, stop)
middle_ix = math.floor((start + stop) / 2)
# move the median to the middle by swapping
arr[median_ix], arr[middle_ix] = arr[middle_ix], arr[median_ix]
# recurse on the left and right halves
mediansort(arr, start, middle_ix)
mediansort(arr, middle_ix + 1, stop)
def find_median(arr, start, stop):
"""Finds the index of a median of the elements in arr[start:stop]."""
numbers = arr[start:stop]
median = sorted(numbers)[len(numbers) // 2]
for i in range(start, stop):
if arr[i] == median:
return i
import random
s = random.randint(10, 100)
arr = [random.randint(0, 1000) for _ in range(s)]
mediansort(arr, 0, len(arr))
print(arr)
The code is supposed to sort ``in place'' by modifying the input array. You may assume that find_median correctly returns the index of the median element in arr[start:stop].
Does Professor Billy's mediansort algorithm work? You may assume that it is called with start = 0 and stop = len(arr).
Solution
No: it will run without error, but \mintinline{python}{arr} may not be sorted when the function exits.
Remember the three things to check when evaluating recursive code: 1) does it have a base case? 2) do the recursive subproblems get smaller and smaller? and 3) assuming that the recursive subcalls do what they say they will, does the algorithm work overall?
In this situation, the third thing does not check out. That is: even if mediansort(arr, start, middle_ix) correctly sorts the numbers in arr[start:middle_ix](and the other call does the same for the right half of the list), this does not mean that arr will be in sorted order over all. We would still need to merge the two sorted halves together into one sorted list.
It might help to look at this another way. On the root call to mediansort, the median is put into its correct position in the sorted order. But on the recursive calls, this is not true. Consider the recursive call on the left half -- during this call, the median of the first \(n/2\) numbers in the list is placed into position \(n/4\)(roughly). This isn't quite what we want -- we want to put the median of the smallest\(n/2\) numbers here. But the first \(n/2\) numbers in the list aren't necessarily the smallest\(n/2\) numbers in the list overall.
Problem #170
Tags: binary search
Consider the version of binary search shown below. This is the same as the code given in lecture, except that a single print statement has been added. This print statement prints the value of stop at the beginning of each call to binary_search.
import math
def binary_search(arr, t, start, stop):
"""
Searches arr[start:stop] for t.
Assumes arr is sorted.
"""
print(stop) # <-- added print statement
if stop - start <= 0:
return None
middle = math.floor((start + stop)/2)
if arr[middle] == t:
return middle
elif arr[middle] > t:
return binary_search(arr, t, start, middle)
else:
return binary_search(arr, t, middle+1, stop)
Suppose binary_search is called on a sorted list with start = 0 and stop = len(n). True or False: the numbers printed must be a non-increasing sequence. That is, if \(x\) is printed before \(y\), then it must be the case that \(x \geq y\).
Solution
True
Problem #171
Tags: asymptotic notation
Suppose \(f_1(n)\) is \(O(n^3)\) and \(\Omega(n)\). Also suppose that \(f_2(n) = O(n^2)\) and \(\Omega(\sqrt n)\).
Consider the function \(f(n) = f_1(n) + f_2(n)\). True or false: it must be the case that \(f(n) = \Omega(n)\).
Solution
True
Problem #172
Tags: asymptotic notation
Consider the function \(f(n) = \sin(12 n) \cdot\cos(n) + 2\). A plot of this function is shown below:
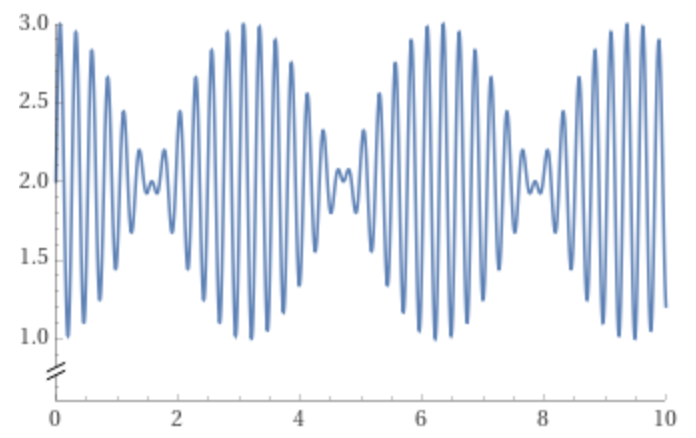
True or False: this function is \(\Theta(1)\).
Solution
True. This function is upper bounded by 3 and lower bounded by 1 for all \(n\), and is therefore \(\Theta(1)\).
Problem #173
Tags: asymptotic notation
Consider again the function \(f(n) = \sin(12n) \cdot\cos(n) + 2\) from the previous problem.
True or False: \(f(n) = O(n^3)\).
Solution
True. We saw that this function is \(\Theta(1)\), but it is also correct to say that it is \(O(n^3)\), though this is not a tight upper bound.
Problem #174
Tags: recurrence relations
Solve the below recurrence, stating the solution in asymptotic notation. Show your work.
Solution
\(\Theta(n)\).
Unrolling several times, we find:
On the \(k\)th unroll, we'll get:
It will take \(\log_2 n\) unrolls to each the base case. Substituting this for \(k\), we get:

Problem #176
Tags: time complexity
import math
def mediansort(arr, start, stop):
"""Claims to sort the array, in-place"""
if stop - start <= 1:
return
# finds the index of the median of arr[start:stop]
median_ix = find_median(arr, start, stop)
middle_ix = math.floor((start + stop) / 2)
# move the median to the middle by swapping
arr[median_ix], arr[middle_ix] = arr[middle_ix], arr[median_ix]
# recurse on the left and right halves
mediansort(arr, start, middle_ix)
mediansort(arr, middle_ix + 1, stop)
Consider the mediansort function from above. Suppose that find_median takes \(\Theta(n)\) time. What is the time complexity of mediansort?
Problem #177
Tags: expected time
What is the expected time complexity of the function below? State your answer using asymptotic notation.
You may assume that math.sqrt and math.log2 take \(\Theta(1)\) time.
import random
import math
def boo(n):
# draw a number uniformly at random from 0, 1, 2, ..., n-1 in Theta(1)
x = random.randrange(n)
if x < math.log2(n):
for i in range(n**2):
print("Very unlucky!")
elif x < math.sqrt(n):
for i in range(n):
print("Unlucky!")
else:
print("Lucky!")
boo(100)
Solution
There are three cases: Case 1) \(x < \log_2 n\); Case 2) \(1 < x < \sqrt n\); and Case 3) \(x \geq\sqrt{n}\).
The probability of Case 1 is \(\log n / n\). The time taken in case 1 is \(\Theta(n^2)\).
The probability of Case 2 is
The time taken in this case is \(\Theta(n)\).
The probability of Case 3 is 1 minus the probability of the sum of the other two cases, which will simply be \(\Theta(1)\):
The time taken is \(\Theta(1)\).
Therefore, the expected time is:
Problem #178
Tags: recurrence relations
State (but do not solve) the recurrence describing the runtime of the following function.
def boo(n):
if n <= 1:
return
for i in range(3):
boo(n/4)
for j in range(n):
print(j)
\( T(n) = \begin{cases} \Theta(1), & n = 1\\ & n > 1 \end{cases}\)
Solution
Even though the recursive calls are made in a for-loop, the basic idea is the same: there will be three recursive calls, each on arrays of size \(n/4\), and thus the recurrence will involve \(3 T(n/4)\). There is \(\Theta(n)\) work done outside the recursive calls, for a full recurrence of \(T(n) = 3 T(n/4) + \Theta(n)\).
Problem #179
Tags: time complexity
What is the expected time complexity of the following function? State your answer using asymptotic notation.
import random
def boo(n):
# draw a number uniformly at random from 0, 1, 2, ..., n-1 in Theta(1)
x = random.randrange(n)
for i in range(x): # <-- note that the range is random!
print(i)
Problem #180
Tags: time complexity
What is the time complexity of the following function? State your answer as a function of \(n\) using asymptotic notation in the simplest form possible. (e.g., \(\Theta(n)\))
import math
def boo(n):
for i in range(n):
for j in range(n**2 + 100, 500*n**3):
for k in range(1_000, math.floor(math.log(n))):
print(i + j + k)
boo(100)
Problem #181
Tags: best and worst case, theoretical lower bounds
Consider the following problem: given two sorted lists, A and B, each containing \(n\) numbers, determine if the two lists share an element in common. That is, determine if there is a number \(x\) which appears in both lists.
Part 1)
What is a tight theoretical lower bound for this problem? Again, you may assume that the lists are both sorted. State your answer in asymptotic notation as a function of \(n\).
Part 2)
(2 points) Briefly (in 50 words or less) describe an algorithm for solving this problem and state its worst case time complexity. To earn full credit, you should give the optimal algorithm, but partial credit will be awarded for sub-optimal solutions. You may write pseudocode if you like, but an explanation in words is also sufficient. Make sure that you only state one algorithm!
Solution
Here's an approach that takes \(\Theta(n)\); it's similar to what we did in lecture for the movie problem.
Start with i = j = 0. If A[i] == A[j], return True, since you've found an element in common. If A[i] > A[j], increment j, otherwise increment i. Takes \(\Theta(n)\) time.
The brute force approach also earns credit: Loop over all pairs, checking if A[i] == B[j] for each pair. This takes \(\Theta(n^2)\) time.
Problem #182
Tags: binary search trees
Draw the binary search tree that results from inserting the following nodes into an initially empty tree, in the order given: 5, 3, 1, 8, 4, 2, 6.
Solution
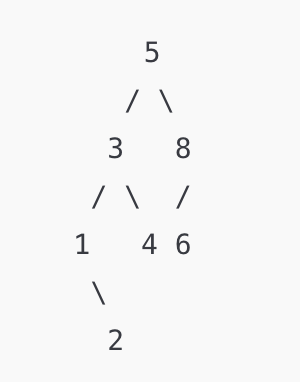
Problem #183
Tags: quickselect
The code for quickselect is shown below. It is the same as the code provided in lecture, except that it contains an added print statement.
import random
def quickselect(arr, k, start, stop):
"""Finds kth order statistic in numbers[start:stop])"""
print("hello world!") # <--- here is the print
pivot_ix = random.randrange(start, stop)
pivot_ix = partition(arr, start, stop, pivot_ix)
pivot_order = pivot_ix + 1
if pivot_order == k:
return arr[pivot_ix]
elif pivot_order < k:
return quickselect(arr, k, pivot_ix + 1, stop)
else:
return quickselect(arr, k, start, pivot_ix)
Suppose quickselect(arr, 3, 0, 10) is called with arr = [5, 2, 8, 3, 1, 6, 9, 7, 4, 0].
Part 1)
What is the fewest number of times that ``hello world!'' can possibly be printed? Your answer should be a number, and not in terms of \(n\).
Part 2)
What is the greatest number of times that ``hello world'' can possibly be printed? Your answer should be a number, and not in terms of \(n\).
Problem #184
Tags: asymptotic notation
Suppose \(f_1(n) = \Omega(g_1(n))\) and \(f_2 = \Omega(g_2(n))\). Define \(f(n) = \max\{ f_1(n), f_2(n) \}\) and \(g(n) = \max\{ g_1(n), g_2(n)\}\).
True or false: it is necessarily the case that \(f(n) = \Omega(g(n))\). In other words, it must be the case that \(\max\{ f_1(n), f_2(n) \} = \Omega( \max\{ g_1(n), g_2(n) \}) \)
Solution
True
Problem #185
Tags: asymptotic notation
Suppose again that \(f_1(n)\) is \(O(n^3)\) and \(\Omega(n)\). Also suppose that \(f_2(n) = O(n^2)\) and \(\Omega(\sqrt n)\).
Consider the function \(g(n) = f_2(n) / f_1(n)\). Give the tightest possible upper bound on \(g(n)\):
\(O(\) \()\)
Problem #186
Tags: time complexity
Suppose bar and baz are two functions. Suppose bar's time complexity is \(\Theta(n^3)\), while baz's time complexity is \(\Theta(n^2)\).
Suppose boo is defined as below:
def boo(n):
if n < 1000:
bar(n)
else:
baz(n)
What is the asymptotic time complexity of boo?
Solution
Asymptotic time complexity concerns the time taken when \(n\) is large. Therefore, it doesn't matter what happens when \(n < 1000\). When \(n \geq 1000\), the time taken is \(\Theta(n^2)\), since that is the time taken by baz.
Problem #187
Tags: asymptotic notation
Let
Write \(f(n)\) in asymptotic notation in the simplest terms possible.
\(f(n) = \Theta(\) )
Problem #188
Tags: time complexity, binary search trees
Suppose a collection of unique numbers is stored in a balanced binary search tree, and that each node in the tree has been given a .size attribute which contains the number of nodes in the subtree rooted at that node. What is the time complexity required of an efficient algorithm for computing the number of elements in the collection which are larger than some threshold, \(t\)?
Solution
\(\Theta(\log{n})\). We can consider the following algorithm: Query for \(t\) in the BST, and define a new variable total for tracking the result. For each step of the recursion, if we go to the left, add the size of the right branch + 1 to the running total. We repeat the above until the query() function finishes running, which will give us exactly the number of elements in the collection which are larger than \(t\). Since we are querying (and adding some constant time updating steps) in a balanced BST, the time complexity for this question will be \(\Theta(\log{n})\).
Problem #189
Tags: time complexity
What is the time complexity of the following function in terms of \(n\)? State your answer using asymptotic notation (e.g., \(\Theta(n)\)) in the simplest terms possible.
def foo(n):
for i in range(n):
for j in range(2023):
for k in range(n - i):
print("DSC40B")
Problem #190
Tags: time complexity
Suppose numbers is a list of integers of length \(n\). What is the time complexity of the following function in terms of \(n\)? State your answer using asymptotic notation (e.g., \(\Theta(n)\)) in the simplest terms possible.
def foo(numbers):
for x in numbers:
r = max(numbers) * min(numbers) * x
print(r)
Problem #191
Tags: best and worst case
The code below takes in two lists, each containing \(n\) integers.
def are_lists_equal(list1, list2):
if len(list1) != len(list2):
return False
for i in range(len(list1)):
if list1[i] != list2[j]:
return False
return True
def foo(list1, list2):
if are_lists_equal(list1, list2):
for i in list1:
print(i)
else:
for i in list1:
for j in list2:
for k in range(len(list1)):
print(i, j, k)
What is the best case time complexity of foo as a function of \(n\)? State your answer using asymptotic notation.
Solution
The best case is where the lists are equal. In this case the time complexity is \(\Theta(n)\). The worst case is when the lists are not equal in which case the time complexity is \(\Theta(n^3)\).
Problem #192
Tags: time complexity
What is the time complexity of the following function in terms of \(n\)? State your answer using asymptotic notation (e.g., \(\Theta(n)\)) in the simplest terms possible.
def foo(n):
i = 1
while i < n**3:
i = i * 2
for j in range(n):
print(i + j)
Problem #193
Tags: mergesort
Below is the merge function from the mergesort algorithm, with an added print statement:
def merge(left, right, out):
"""Merge sorted arrays, store in out."""
print(len(left))
print(len(right))
left.append(float('inf'))
right.append(float('inf'))
left_ix = 0
right_ix = 0
for ix in range(len(out)):
if left[left_ix] < right[right_ix]:
out[ix] = left[left_ix]
left_ix += 1
else:
out[ix] = right[right_ix]
right_ix += 1
Suppose this version of merge is used in mergesort, and mergesort is called on the following list:
[6, 2, 7, 1, 9, 3, 8, 5].
If all of the numbers that are printed are added up, what will the sum be?
Problem #194
Tags: time complexity, binary search trees
Suppose a collection of \(n\) numbers is stored in a balanced binary search tree. What is the time complexity required of an efficient algorithm to calculate the mean of the collection? State your answer as a function of \(n\) in asymptotic notation.
Problem #195
Tags: asymptotic notation
Suppose again that \(f_1(n)\) is \(O(n^3)\) and \(\Omega(n^2)\). Also suppose that \(f_2(n)\) is \(O(n^4)\) and \(\Omega(n)\).
Consider the function \(g(n) = f_2(n) / f_1(n)\). Give the tightest possible upper bound on \(g(n)\):
\(O(\) \()\)
Problem #196
Tags: loop invariants
Consider this code which partitions a list in a special way:
def is_even(i):
"""Returns True if i is even, False otherwise."""
return i % 2 == 0
def mystery_partition(numbers):
def swap(i, j):
numbers[i], numbers[j] = numbers[j], numbers[i]
barrier_ix = 0
for i in range(len(numbers)):
if is_even(numbers[i]):
swap(i, barrier_ix)
if numbers[barrier_ix] > numbers[0]:
swap(0, barrier_ix)
barrier_ix += 1
lst = [1, 5, 3, 7, 2, 4, 8, 5, 9, 6, 100]
mystery_partition(lst)
print(lst)
Which of the following loop invariants are true for this code? Select all that apply.
Note: any statement about an empty set or list is considered to be automatically true.
Solution
1st option: After each iteration of the for loop, all numbers in numbers[:barrier_ix] are even.
3rd option: After each iteration of the for loop, numbers[0] is greater than or equal to all numbers in numbers[:barrier_ix].
Problem #197
Tags: sorted structure
A rotated sorted array is an array that is the result of taking a sorted array and moving a contiguous section from the front of the array to the back of the array. For example, the array [5, 6, 7, 1, 2, 3, 4] is a rotated sorted array: it is the result of taking the sorted array [1, 2, 3, 4, 5, 6, 7] and moving the first 4 elements, [1, 2, 3, 4], to the back of the array. Sorted arrays are also rotated sorted arrays, technically speaking, since you can think of a sorted array as the result of taking the sorted array and moving the first 0 elements to the back.
The function below attempts to find the value of the minimum element in a rotated sorted array. It is given the array arr and the indices start and stop which indicate the range of the array that should be searched. One line in the function has been left blank.
import math
def find_minimum_in_rotated_sorted(arr, start, stop):
"""
Searches arr[start:stop] for the smallest element.
Assumes arr is a rotated sorted array.
"""
if stop < start:
return arr[0]
if stop == start:
return arr[start]
mid = (start + stop) // 2
if ________________:
return arr[mid + 1]
if arr[start] < arr[mid]:
return find_minimum_in_rotated_sorted(arr, mid, stop)
else:
return find_minimum_in_rotated_sorted(arr, start, mid - 1)
What should be filled in the blank line to make this function work correctly?
Solution
5th option: arr[middle] > arr[middle+1]
Problem #198
Tags: asymptotic notation
Suppose \(f_1(n)\) is \(O(n^3)\) and \(\Omega(n^2)\). Also suppose that \(f_2(n)\) is \(O(n^4)\) and \(\Omega(n)\).
Consider the function \(f(n) = f_1(n) + f_2(n)\). True or false: it must be the case that \(f(n) = \Omega(n^2)\).
Solution
True
Problem #199
Tags: verifying recursion
Consider the following function which attempts to compute the maximum of a list of numbers.
import math
def maximum(numbers):
n = len(numbers)
if n == 0:
return 0
middle = math.floor(n / 2)
return (
maximum(numbers[:middle])
+
maximum(numbers[middle:])
)
Is this code guaranteed to work for all non-empty lists?
You should adopt the convention that the maximum of an empty list is \(-\infty\).
Solution
2nd option: No: it may recurse infinitely.
Problem #200
Tags: time complexity
What is the expected time complexity of the function below? State your answer using asymptotic notation.
import random
def foo(n):
# draw a number uniformly at random from 0, 1, 2, ..., n-1 in Theta(1) time
x = random.randrange(n)
if x < 20:
for i in range(n**3):
print("Very unlucky!")
elif x < n / 2:
for i in range(n):
print("Unlucky!")
else:
print("Lucky!")
Problem #201
Tags: recurrence relations
Solve the below recurrence, stating the solution in asymptotic notation. You do not need to show your work (and your work won't be graded for partial credit, so be careful!).
Solution
\(\Theta(n)\).
Unrolling several times, we find:
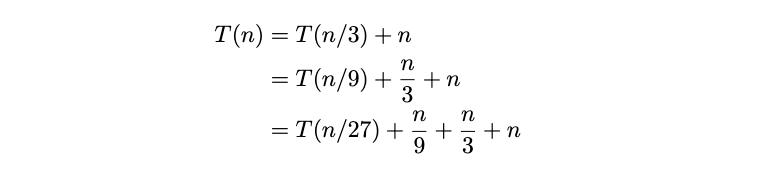
On the \(k\)th unroll, we'll get:
It will take \(\log_3 n\) unrolls to each the base case. Substituting this for \(k\), we get:

Problem #202
Tags: recurrence relations
State (but do not solve) the recurrence describing the runtime of the following function.
def foo(n):
if n <= 1:
return
foo(n // 2)
for j in range(n):
print(j)
foo(n // 2)
Problem #203
Tags: time complexity
What is the time complexity of the following function in terms of \(n\)? State your answer using asymptotic notation (e.g., \(\Theta(n)\)) in the simplest terms possible.
import math
def foo(n):
for i in range(3 * n**3 + 5 * n * math.ceil(math.log(n))):
for j in range(math.floor(math.sqrt(n))):
print(i + j)
for k in range(n**2):
print(k * i)
Problem #204
Tags: theoretical lower bounds
In this problem, assume that \(A\) and \(B\) are sorted lists, each containing \(n\) numbers.
Part 1)
What is the best possible (worst case) time complexity of any algorithm for finding the smallest difference between a number in \(A\) and a number in \(B\)?
Part 2)
What is the best possible (worst case) time complexity of any algorithm for finding the biggest difference between a number in \(A\) and a number in \(B\)?
Problem #205
Tags: asymptotic notation
Let \(f(n) = 3n^2 \log n\). True or False: \(f(n) = O(n^3)\).
Solution
True
Problem #206
Tags: time complexity
Suppose bar_1, bar_2 and bar_3 are three functions. Suppose bar_1's time complexity is \(\Theta(n)\), bar_2's time complexity is \(\Theta(n^2)\), and bar_3's time complexity is \(\Theta(n^3)\).
Suppose foo is defined as below:
def foo(n):
if n < 2023:
bar_1(n**3)
elif n == 2023:
bar_3(n**2)
else:
bar_2(n)
What is the asymptotic time complexity of foo?
Solution
Asymptotic time complexity concerns the time taken when \(n\) is large. Therefore, it doesn't matter what happens when \(n < 1000\). When \(n \geq 1000\), the time taken is \(\Theta(n^2)\), since that is the time taken by bar_2.
Problem #207
Tags: asymptotic notation
Let
Define \(f(n) = f_1(n) \times f_2(n) \times f_3(n)\). What is \(f(n)\), in asymptotic notation, in simplest terms possible?
Problem #208
Tags: asymptotic notation
Consider the function defined below:
True or False: \(f(n) = \Theta(n)\).
Solution
True