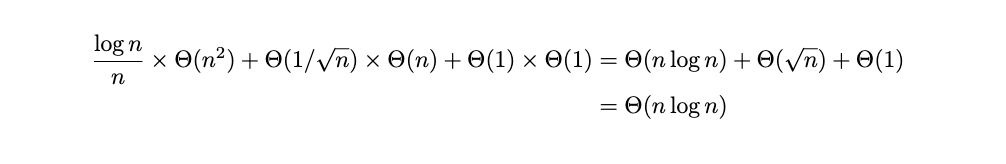DSC 40B – Theoretical Foundations of Data Science II

Problems tagged with "expected time"

Problem #009

Tags: expected time

What is the expected time complexity of the function below?


import random

def foo(n):
    # draw a random number uniformly from 0, 1, 2, ..., 99
    # in constant time
    x = random.randrange(100)
    for i in range(x):
        for j in range(n):
            print("Here!")
Solution

\(\Theta(n)\). Note that in this question, the range of \(x\) is between 0 and 99. Therefore the outer loop will run a constant number of times no matter what \(x\) is. Then we can focus on the inner loop, which runs for \(n\) times the print() operation, which is \(\Theta(n)\) time. Therefore, the expected time complexity for this piece of code is \(\Theta(n)\).

Problem #010

Tags: expected time

What is the expected time complexity of the function below?


import random

def foo(n):
    # draw a number uniformly at random from 0, 1, 2, ..., n-1
    # in constant time
    x = random.randrange(n)
    if x < 100:
        for j in range(n**2):
            print(j)
Solution

\(\Theta(n)\). The for loop is only executed if \(x\) is less than 100, therefore we can write the expected time as (ignoring constants \(c\)):

\[ f(n) = \frac{1}{n}\bigg(\sum_{i = 0}^{99} n^2 + \sum_{i = 100}^{n - 1} 1 \bigg)= \frac{1}{n}\cdot(\Theta(n^2) + \Theta(n)) = \Theta(n). \]

Problem #032

Tags: expected time

What is the expected time complexity of the following function?


import random

def foo(n):
    for i in range(n):
        # draw a number uniformly at random from 0, 1, 2, ..., n-1 in Theta(1)
        x = random.randrange(n)
        for j in range(x):
            print(j)
Solution

\(\Theta(n^2)\). For this function, the outer loop wil execute \(n\) times no matter what, hence we only have to find what the expected time complexity for the inner loop is, then combine that together with the outer loop. For the inner loop, the expected time complexity is

\[\frac{1}{n}\sum_{i = 1}^{n - 1} i = \frac{1}{n}\cdot\Theta(n^2) = \Theta(n). \]

Then, the expected complexity for the whole function will be

\[\Theta(n) \times\Theta(n) = \Theta(n^2). \]

Problem #037

Tags: expected time

What is the expected time complexity of the function below?


import random

def foo(n):
    # draw a number uniformly at random from 0, 1, 2, ..., n-1 in Theta(1)
    x = random.randrange(n)
    if x < math.sqrt(n):
        for j in range(n):
            print(j)
Solution

\(\Theta(\sqrt n)\). Since the for loop only executes when \(x\) is less than \(\sqrt{n}\), the expected time complexity is

\[\frac{1}{n}\bigg(\sum_{i = 1}^{\lfloor \sqrt{n} \rfloor} n + \sum_{i = \lceil \sqrt{n} \rceil}^{n - 1} 1 \bigg)\approx\frac{1}{n}(n \sqrt{n} + (n - \sqrt{n})) = \Theta(\sqrt{n}). \]

Problem #059

Tags: expected time

What is the expected time complexity of the following function? State your answer using asymptotic notation.


import random

def foo(n):
    x = random.randrange(n)

    if x < 8:
        for j in range(n**3):
            print(j)
    else:
        for j in range(n):
            print(j)
Solution

\(\Theta(n^2)\). The expected time complexity for this function is

\[\frac{1}{n}\bigg(\sum_{i = 0}^{7} n^3 + \sum_{i = 8}^{n - 1} n \bigg)= \frac{1}{n}(\Theta(n^3) + \Theta(n^2)) = \Theta(n^2). \]

Problem #064

Tags: expected time

What is the expected time complexity of the function below? State your answer using asymptotic notation.

You may assume that math.sqrt and math.log take \(\Theta(1)\) time. math.log computes the natural log.


import random
import math

def foo(n):
    # draw a number uniformly at random from 0, 1, 2, ..., n-1 in Theta(1)
    x = random.randrange(n)

    if x < math.log(n):
        for j in range(n**2):
            print(j)
    elif x < math.sqrt(n):
        print('Ok!')
    else:
        for i in range(n):
            print(i)
Solution

\(\Theta(n \log n)\) There are three cases: Case 1) \(x < \log n\); Case 2) \(\log n \geq x < \sqrt n\); and Case 3) \(x \geq\sqrt{n}\).

The probability of Case 1 is \(\log n / n\). The time taken in case 1 is \(\Theta(n^2)\).

The probability of Case 2 is

\[\frac{\sqrt n}{n} - \frac{\log n}{n} = \Theta(\sqrt n / n) = \Theta(1/\sqrt n). \]

The time taken in this case is \(\Theta(1)\).

The probability of Case 3 is 1 minus the probability of the sum of the other two cases, which will simply be \(\Theta(1)\):

\[ 1 - \Theta((\log n) / n) - \Theta(1 / \sqrt{n}) = \Theta(1) \]

Therefore, the expected time is:

\[\begin{aligned} \frac{\log n}{n} \times \Theta(n^2) + \Theta(1/\sqrt n) \times \Theta(1) + \Theta(1) \times \Theta(n) &= \Theta(n \log n) + \Theta(1 / \sqrt n) + \Theta(n) \\ &= \Theta(n \log n) \end{aligned}\]

Problem #088

Tags: expected time

What is the expected time complexity of the function below?

You may assume that math.sqrt takes \(\Theta(1)\) time.


import random
import math

def foo(n):
    # draw a number uniformly at random from 0, 1, 2, ..., n-1 in Theta(1)
    x = random.randrange(n)

    if x < math.sqrt(n):
        for j in range(n):
            print(j)
    elif x < n//2:
        print('Ok!')
    else:
        for i in range(n**2):
            print(i)
Solution

\(\Theta(n^2)\). The expected time complexity for this function is

\[ f(n) = \frac{1}{n}\bigg(\sum_{i = 1}^{\lfloor \sqrt{n} \rfloor} n + \sum_{i = \lceil \sqrt{n} \rceil}^{\lfloor n/2 \rfloor} 1 + \sum_{i = \lceil n/2 \rceil}^{n - 1} n^2 \bigg) = \frac{1}{n}(\Theta(n \sqrt{n}) + \Theta(n) + \Theta(n^3)) = \Theta(n^2). \]

Problem #089

Tags: expected time

What is the expected time complexity of the function below?


import random

def foo(n):
    # draw a random number uniformly from 0, 1, 2, ..., n-1
    # in constant time
    x = random.randrange(n)
    for i in range(x):
        for j in range(n):
            print("Here!")
Solution

\(\Theta(n^2)\). The inner loop is not random, and the time complexity of it is always \(\Theta(n)\). Therefore the expected time complexity of this function will be (using the arithmetic sequence sum formula)

\[\frac{1}{n}\sum_{i = 0}^{n - 1} i \times\Theta(n) = \Theta(n^2). \]

Problem #177

Tags: expected time

What is the expected time complexity of the function below? State your answer using asymptotic notation.

You may assume that math.sqrt and math.log2 take \(\Theta(1)\) time.


import random
import math

def boo(n):
    # draw a number uniformly at random from 0, 1, 2, ..., n-1 in Theta(1)
    x = random.randrange(n)

    if x < math.log2(n):
        for i in range(n**2):
            print("Very unlucky!")
    elif x < math.sqrt(n):
        for i in range(n):
            print("Unlucky!")
    else:
        print("Lucky!")

boo(100)

Solution

There are three cases: Case 1) \(x < \log_2 n\); Case 2) \(1 < x < \sqrt n\); and Case 3) \(x \geq\sqrt{n}\).

The probability of Case 1 is \(\log n / n\). The time taken in case 1 is \(\Theta(n^2)\).

The probability of Case 2 is

\[\frac{\sqrt n}{n} - \frac{\log_2 n}{n} = \Theta(\sqrt n / n) = \Theta(1/\sqrt n). \]

The time taken in this case is \(\Theta(n)\).

The probability of Case 3 is 1 minus the probability of the sum of the other two cases, which will simply be \(\Theta(1)\):

\[ 1 - \Theta(1 / n) - \Theta(1 / \sqrt{n}) = \Theta(1). \]

The time taken is \(\Theta(1)\).

Therefore, the expected time is: