DSC 40B – Theoretical Foundations of Data Science II
Midterm 02
Practice problems for topics on Midterm 02. See also the Sample Midterm 02 and its solutions.
Tags in this problem set:
Problem #095
Tags: hashing
Suppose a hash table is constructed so that collisions are resolved through chaining. The hash table has \(10\) bins, and 100 items are inserted into the hash table.
True or False: it is possible for one of the bins to contain all 100 items.
Solution
True.
Problem #096
Tags: hashing
Suppose a hash table in constructed so that collisions are resolved through chaining. The hash table has a number of bins \(k\) that is \(\Theta(n)\), where \(n\) is the number of elements being stored in the hash table; that is, the hash table grows as more elements are inserted.
Suppose the hash function uses only the first \(k / 2\) bins of the hash table, but appears to hash items into these bins evenly.
What is the expected time complexity of a membership query on this hash table? State your answer in asymptotic notation in terms of the number of elements in the hash table, \(n\).
Solution
\(\Theta(1)\) Since only \(k/2\) bins are being used, the expected number of elements within each bin is \(n / (k/2) = 2n / k\). But since \(k = \Theta(n)\), this is just \(\Theta(1)\).
Problem #097
Tags: hashing
Consider the code below:
def intersection(A, B):
common = set()
for x in A:
if x in B:
common.add(x)
return common
What is the expected time complexity of this code if A and B are Python sets (hash tables) with \(n\) elements each? State your answer as a function of \(n\) using asymptotic notation. You may assume that the hash function used is ``good'' in that it hashes evenly (that is, it satisfies the simple universal hashing assumption).
Solution
\(\Theta(n)\)
Problem #098
Tags: graph theory
An undirected graph has 5 nodes. What is the greatest number of edges it can have?
Solution
10
Problem #099
Tags: graph theory
A directed graph has 10 edges. What is the smallest number of nodes it can have?
Solution
4
Problem #100
Tags: connected components, graph theory
An undirected graph with 20 nodes and 30 edges has three connected components: \(A\), \(B\), and \(C\). Connected component \(A\) has 7 nodes. What is the smallest number of edges it can have?
Solution
6
Problem #101
Tags: graph theory
Let \(v = \{a, b, c, d, e, f, g\}\) and \(E = \{(a,g), (b,d), (d, e), (f, d)\}\). How many connected components does the undirected graph \(G =(V, E)\) have?
Solution
3
Problem #102
Tags: graph theory
Let \(G = (V, E)\) be a directed graph with \(|V| > 1\). Suppose that every node in \(G\) is reachable from every other node. True or False: each node in the graph must have an out-degree of at least one and an in-degree of at least one.
Solution
True.
Problem #103
Tags: shortest paths
Let \(G\) be an undirected graph, and let \(u, v,\) and \(z\) be three nodes in the graph. Consider the problem of finding a shortest path from \(u\) to \(v\) which passes through node \(z\).
True or False: a shortest path from \(u\) to \(v\) passing through \(z\) may include node \(u\) twice.
Solution
True.
Consider the "chain" graph A - B - C - D - E. The shortest path from C to E that passes through B is C - B - C - D - E. It passes through C twice.
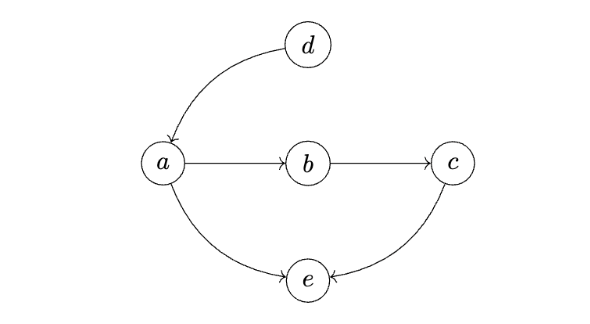
Problem #104
Tags: graph representations
An isolated node in an undirected graph is a node that has no neighbors.
Suppose a graph \(G = (V, E)\) is represented using an adjacency matrix. What is the best possible worst-case time complexity of an efficient algorithm for computing the number of isolated nodes in the graph? State your answer as a function of \(|V|\) and \(|E|\) using asymptotic notation.
Solution
\(\Theta(V^2)\)
Problem #105
Tags: breadth first search
Consider running a breadth-first search (BFS) on the graph shown below, using node \(s\) as the source and adopting the convention that neighbors are produced in ascending order by label.
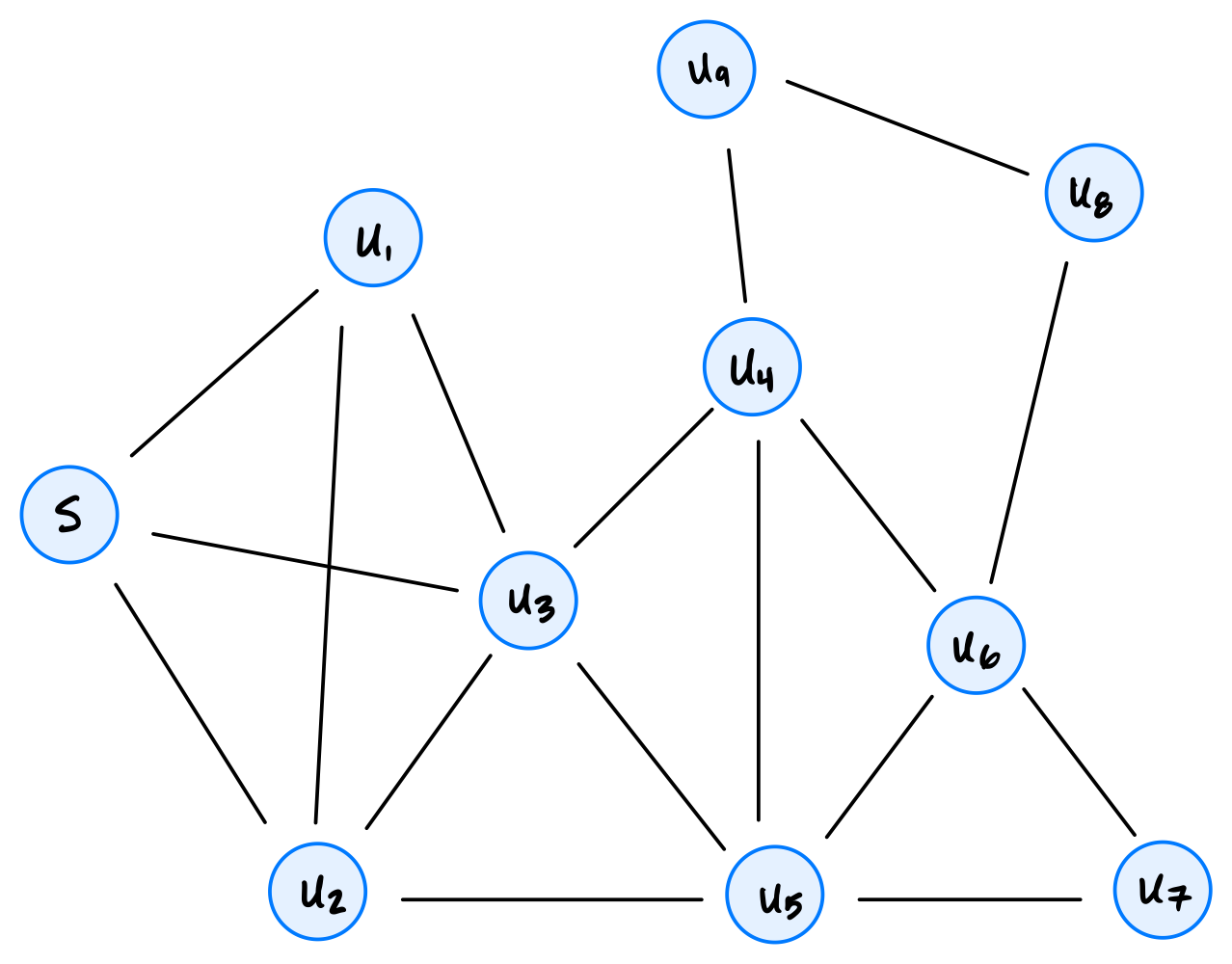
How many nodes will be popped from the queue before node \(u_8\) is popped?
Solution
9
Problem #106
Tags: breadth first search, shortest paths
Suppose that a breadth-first search on an undirected graph \(G\) is paused and the queue is printed. Suppose that every node in the queue is either distance 5 from the source, or distance 6. At this moment, node \(u\) is undiscovered.
True or False: it is possible that node \(u\) is distance 4 from the source.
Solution
False.
Problem #107
Tags: breadth first search
Suppose a breadth-first search (BFS) is performed in order to calculate a dictionary of shortest path distances, dist, from a source node \(s\) to all nodes reachable from \(s\) in an undirected graph \(G = (V, E)\).
Suppose node \(u\) is a node in \(G\), and \(v_1\) and \(v_2\) are two neighbors of node \(u\). Assume that \(u\) is reachable from \(s\).
Part 1)
What is the largest that \(|\)dist[v_2] - dist[v_1]\(|\) can be?
Solution
2
Part 2)
What is the smallest that \(|\)dist[v_2] - dist[v_1]\(|\) can be?
Solution
0
Problem #108
Tags: breadth first search
Define a circle graph with \(n\) nodes to be an undirected graph \(G = (V, E)\) with nodes \(u_1, u_2, \ldots, u_n\) and edges \((u_1, u_2), (u_2, u_3), \ldots, (u_{n-1}, u_n)\), along with one additional edge \((u_n, u_1)\) completing the cycle. An example of a circle graph with 6 nodes is shown below:
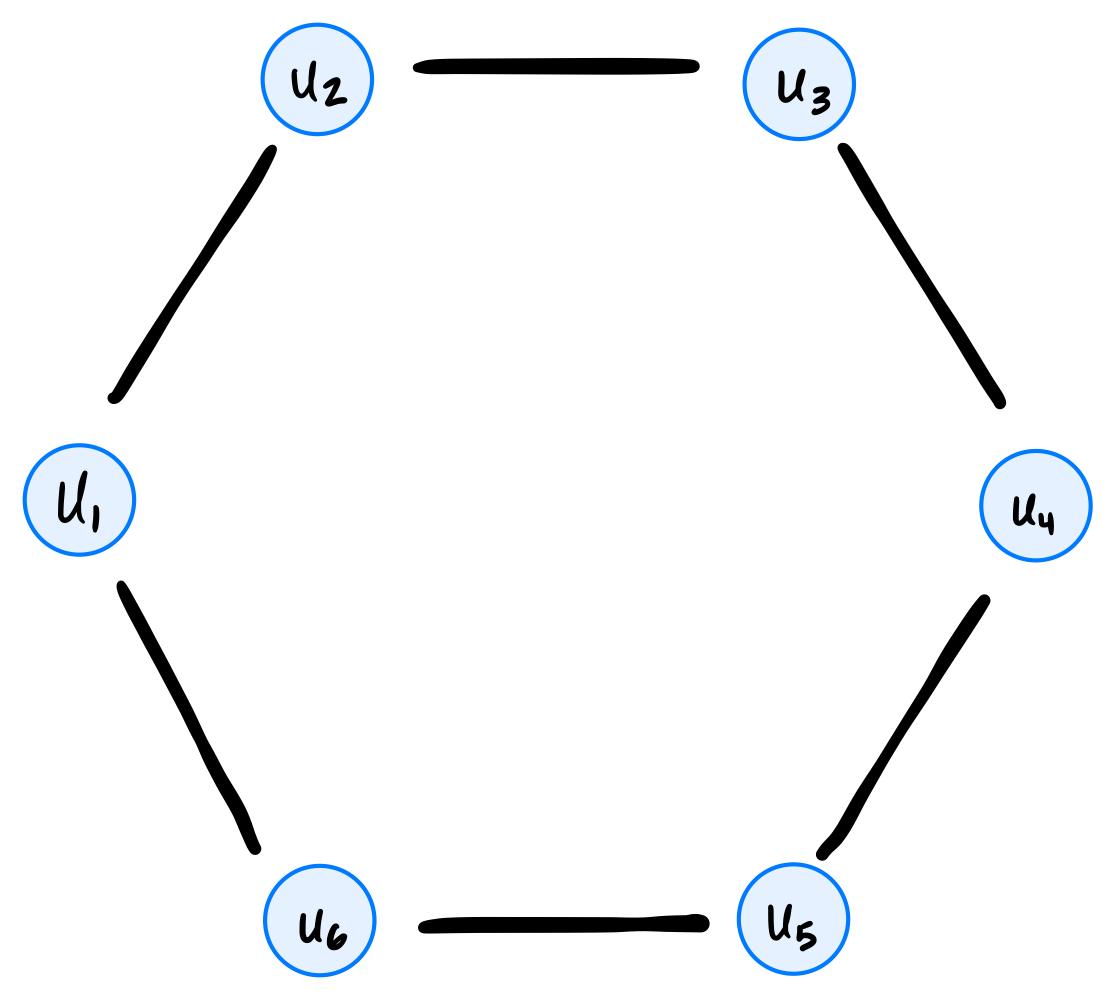
What is the time complexity of breath-first search when run on a circle graph with \(n\) nodes? State your answer as a function of \(n\) using asymptotic notation.
Solution
\(\Theta(n)\)
Problem #109
Tags: aggregate analysis, breadth first search
Consider the code below, which is a modification of the code for bfs given in lecture:
from collections import deque
def modified_full_bfs(graph):
status = {node: 'undiscovered' for node in graph.nodes}
for node in graph.nodes:
if status[node] == 'undiscovered':
modified_bfs(graph, node, status)
def modified_bfs(graph, source, status=None):
"""Start a BFS at `source`."""
if status is None:
status = {node: 'undiscovered' for node in graph.nodes}
status[source] = 'pending'
pending = deque([source])
# while there are still pending nodes
while pending:
u = pending.popleft()
for v in graph.neighbors(u):
# explore edge (u,v)
if status[v] == 'undiscovered':
status[v] = 'pending'
# append to right
pending.append(v)
for z in graph.nodes: # <----- new line!
print(z, status[z]) # <----- new line!
status[u] = 'visited'
Notice the two new lines; these lines print all node statuses any time that an undiscovered node has been found.
What is the time complexity of this modified modified_full_bfs? State your answer in asymptotic notation in terms of the number of nodes, \(|V|\), and the number of edges, \(|E|\). You may assume that the graph is represented using an adjacency list, and that it is connected.
Solution
\(\Theta(V^2)\).
First, the newly-added code (the for z in graph.nodes loop), takes \(\Theta(V)\) time each time the loop is encountered. The crux is: how many times is that loop encountered?
This loop is encountered every time we add a node to the queue (except for the root node, which we add to the queue right at the beginning of BFS). Since this is a connected graph, each node will get added to the pending queue exactly once, meaning that this new code is encountered exactly\(V-1\) times (the \(-1\) is subtracting the root node; the loop isn't encountered when we change it to pending).
Since the new code takes \(\Theta(V)\) time each time it's encountered, and since it's encountered \(\Theta(V)\) times, the total time complexity of the loop is \(\Theta(V^2)\).
You might wonder why the time complexity isn't \(\Theta(VE)\), since the new code is within the loop that ``explores'' each edge in the graph, and we know that it makes a total of \(2|E|\) iterations when the graph is undirected. This is true, but recognize that the new code only executes when the if-statement before it is True, and this will happen on only a subset of the \(2|E|\) iterations. In fact, it will happen exactly \(|V|-1\) times, as we argued above.
Problem #110
Tags: breadth first search
Consider calling full_bfs on a directed graph, and recall that full_bfs will make calls to bfs until all nodes have been marked as visited.
True or False: the number of calls made to bfs depends on the order in which graph.nodes produces the graph's nodes. That is, if nodes are produced in a different order, the number of calls to bfs may be different.
Solution
True.
Problem #111
Tags: depth first search, start and finish times
Suppose a depth-first search (DFS) is run on the graph shown below using node \(s\) as the source and adopting the convention that a node's neighbors are produced in ascending order of their label.
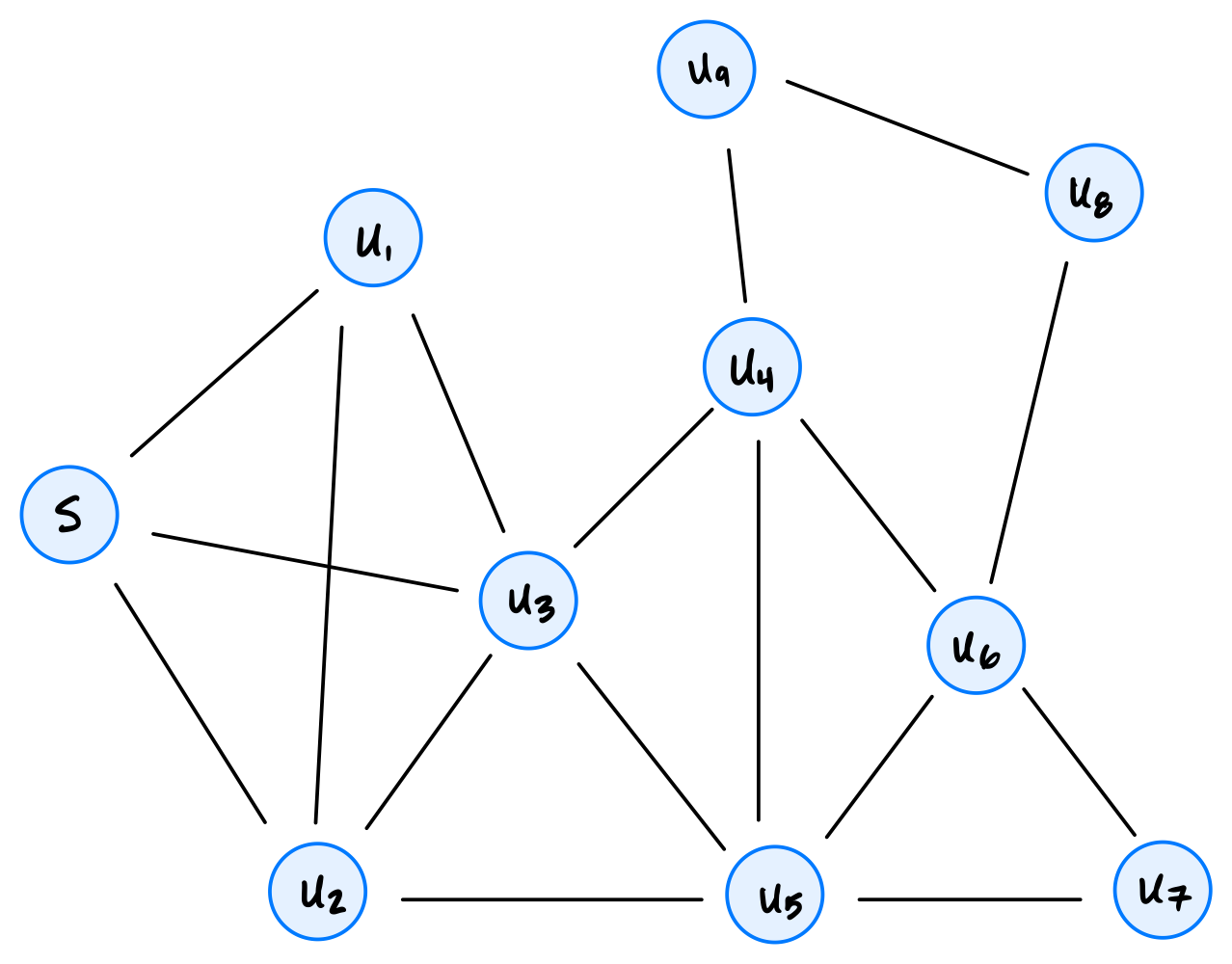
Part 1)
What will be the start time of node \(u_7\)?
Solution
8
Part 2)
What will be the finish time of node \(u_7\)?
Solution
9
Part 3)
Which node will be the DFS predecessor of node \(u_7\)?
Solution
\(u_6\)
Problem #112
Tags: depth first search, start and finish times
Let \(G\) be a graph, and suppose \(s\), \(u\), and \(v\) are three nodes in the graph.
Suppose a depth-first search (DFS) is run on \(G\) using node \(s\) as the source and adopting the convention that a node's neighbors are produced in ascending order by label. During this DFS, start and finish times are computed. Suppose it is found that:
Now suppose another DFS is run using node \(s\) as the source, but adopting a different convention about the order in which neighbors are produced. Suppose new_start and new_finish are the start and finish times found by this second DFS. True or False: it must be that
Solution
False.
Problem #113
Tags: topological sorting
Consider the graph \(G = (V, E)\) with \(V = \{a, b, c\}\) and \(E = \{(a, b)\}\).
How many valid topological sorts of this graph are there?
Solution
3
Problem #114
Tags: depth first search
Suppose we define a forward-looking graph with \(n\) nodes to be the directed graph \(G = (V, E)\) with nodes \(u_1, \ldots, u_n\) and the edge \((u_i, u_j)\) if and only if \(i < j\). An example of such a graph with 4 nodes is shown below.
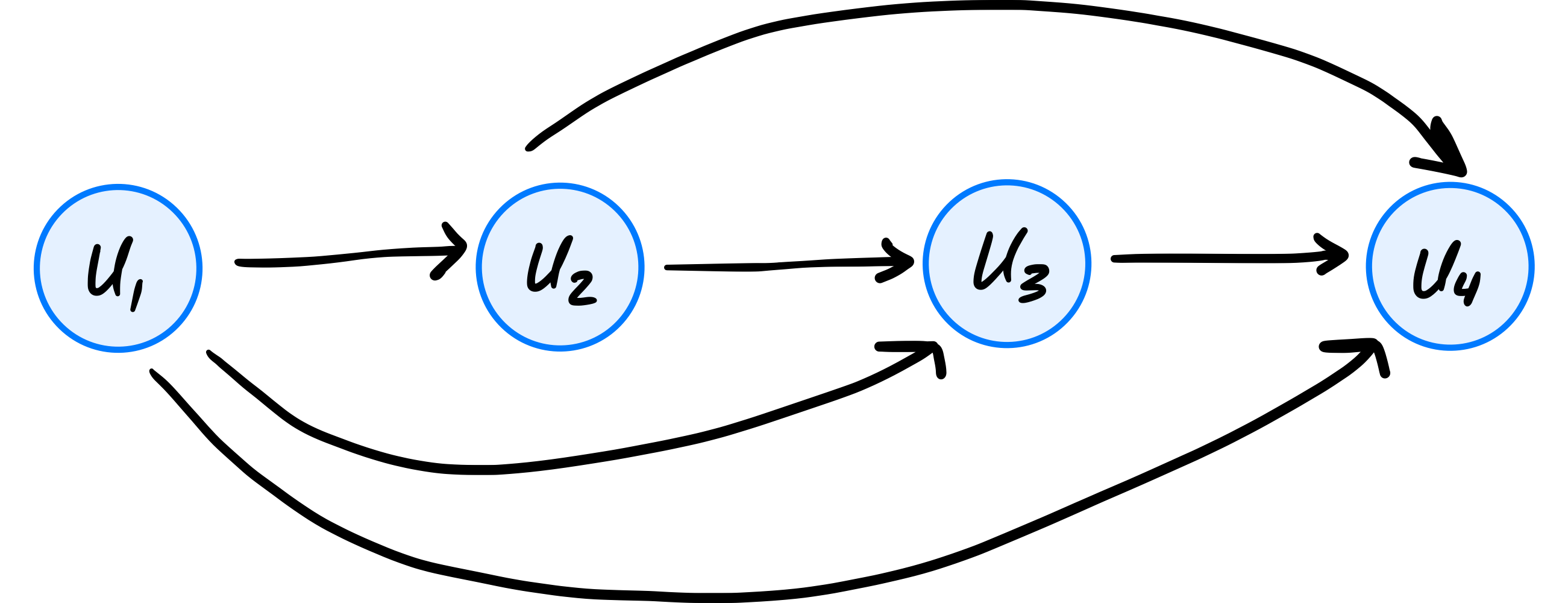
What is the time complexity of depth-first search when run on a forward-looking graph with \(n\) nodes, using node \(u_1\) as the source? State your answer as a function of \(n\) using asymptotic notation.
Solution
\(\Theta(n^2)\)
Problem #115
Tags: depth first search, aggregate analysis
Suppose an undirected graph \(G = (V, E)\) is a tree with 33 edges. Suppose a node \(s\) is used as the source of a depth-first search.
Including the root call of dfs on node \(s\), how many calls to dfs will be made?
Solution
34
Problem #116
Tags: depth first search, breadth first search
Let \(G = (V, E)\) be an undirected tree.
Suppose breadth-first search (BFS) and depth-first search (DFS) are each run on the graph using the same source node. True or False: for any node \(u\) in the graph, the BFS predecessor of \(u\) and the DFS predecessor of \(u\) must be the same.
Solution
True.
Problem #117
Tags: bellman-ford
Recall that the outer loop of the Bellman-Ford algorithm without early stopping loops for a fixed number of iterations, while the inner loop iterates over each edge of the graph.
Suppose Bellman-Ford with early stopping is run on the graph below using node \(s\) as the source:
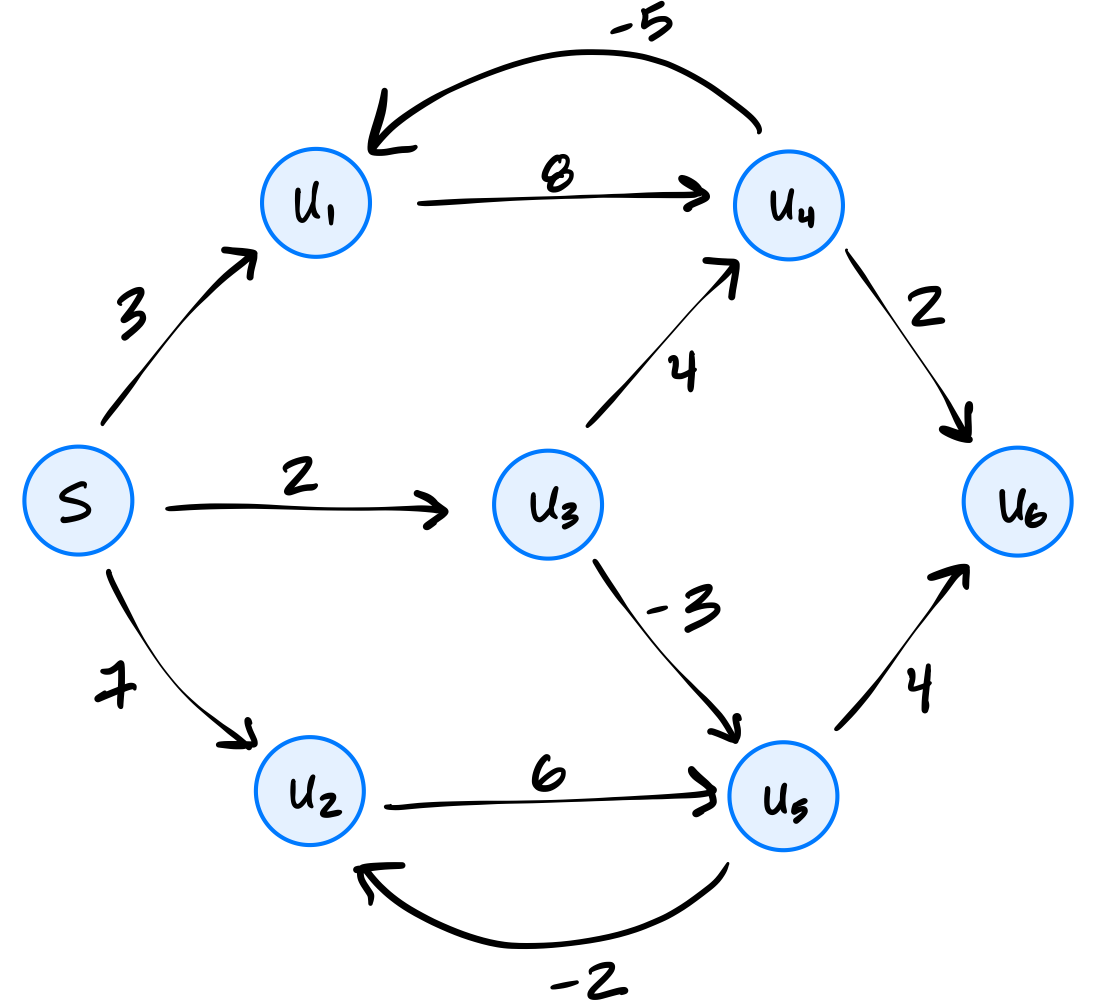
What is the fewest number of iterations of the outer loop that can possibly be performed?
Solution
2
Problem #118
Tags: bellman-ford
Recall that the Bellman-Ford algorithm keeps track of the estimated shortest path distance from the source to each node in the graph. These estimates are updated, and eventually become correct, provided that the graph has no negative cycles.
Suppose the Bellman-Ford algorithm is run on the graph below using node \(s\) as the source.
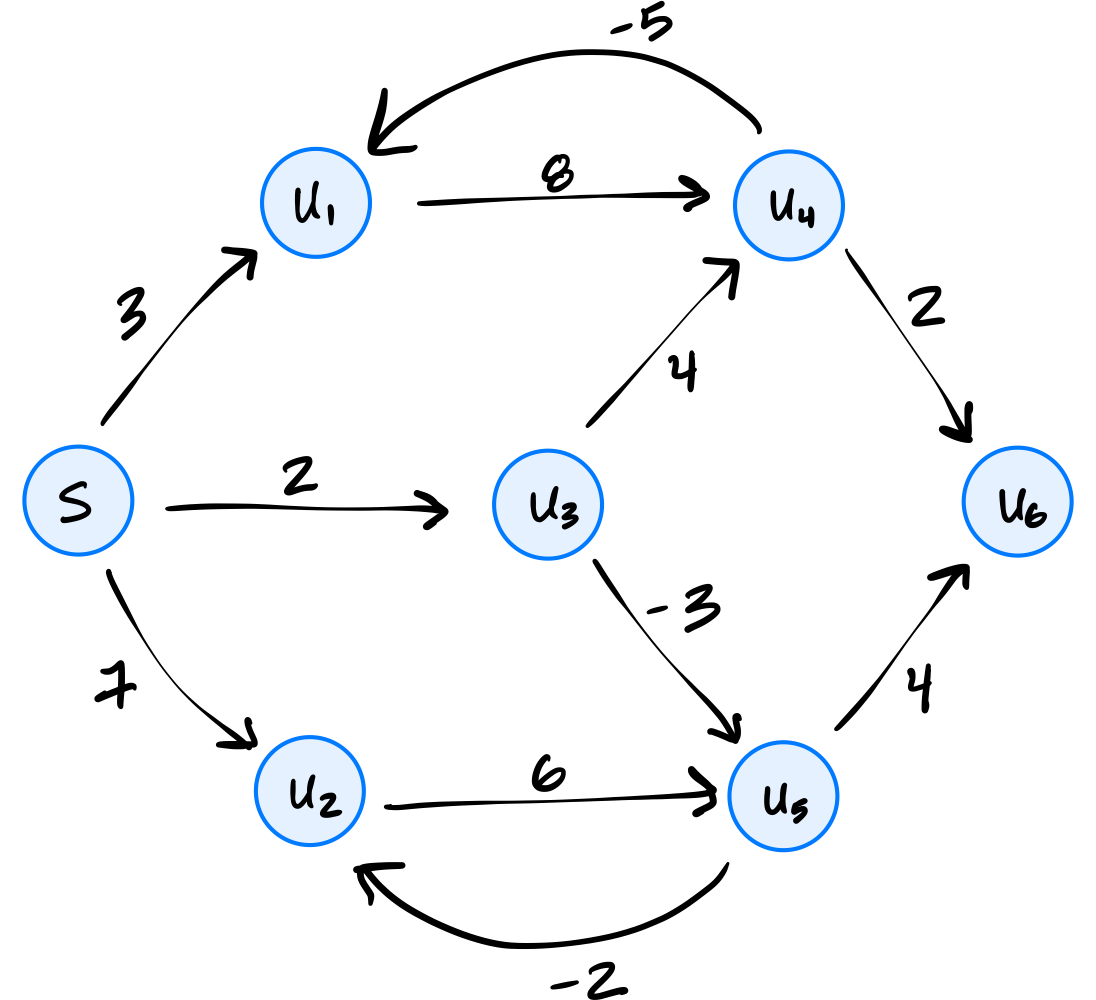
After 2 iterations of the outer loop, which of the nodes listed below are guaranteed to have correct estimated shortest path distances (no matter the order in which graph.nodes produces the graph's nodes)? Select all that apply.
Solution
\(u_3\), \(u_4\), and \(u_5\) are guaranteed to have correct estimated shortest path distances after 2 iterations of the outer loop. \(s\) is guaranteed to have a correct estimated shortest path distance after 1 iteration of the outer loop.
Problem #119
Tags: bellman-ford
Suppose the Bellman-Ford algorithm is run on a graph \(G\) that does not contain negative cycles. Let \(u\) be an arbitrary node in the graph, and assume that \(u\) is reachable from the source.
True or False: \(u\)'s estimated distance can change multiple times during the algorithm's execution.
Solution
True.
Problem #120
Tags: hashing
What is the expected time complexity of the code shown below, assuming that numbers is a Python list? Express your answer as a function of \(n\) using asymptotic notation (e.g., \(\Theta(n)\)).
def foo(numbers):
"""Assume that `numbers` is a list containing n numbers."""
# counts is a Python dictionary, which is implemented using hash table
counts = {}
for x in numbers:
for y in numbers:
diff = abs(x - y)
if diff not in counts:
counts[diff] = 1
else:
counts[diff] = counts[diff] + 1
return counts
foo([1, 2, 3, 4])
Solution
\(\Theta(n^2)\)
Problem #121
Tags: hashing
Suppose a hash table with \(n/2\) bins stores \(n\) elements, and suppose that when the next element is inserted into the hash table, a ``grow'' will be triggered. That is, the insertion will cause the hash table to resize to \(n\) bins containing the same \(n + 1\) elements, plus the newly-added element.
What will be the time complexity of this single insertion operation that causes the table to grow?
Solution
\(\Theta(n)\)
Problem #122
Tags: graph theory
An undirected graph \(G = (V, E)\) has 23 nodes and 2 connected components. What is the smallest number of edges it can have?
Solution
21
Problem #123
Tags: connected components, graph theory
Let \(G = (V, E)\) be an undirected graph, and suppose that \(u, v, \) and \(w\) are three nodes in \(V\). Suppose that \(u\) and \(v\) are in the same connected component, but \(u\) and \(w\) are not in the same connected component. True or False: it is possible that \(v\) and \(w\) are in the same connected component.
Solution
False.
Problem #124
Tags: graph theory
Let \(G\) be an undirected graph. Suppose that the degree of every node in the graph is greater than or equal to one. True or False: \(G\) must be connected.
Solution
False.
Problem #125
Tags: graph theory
What is the out-degree of node \(u\) in the graph shown below?
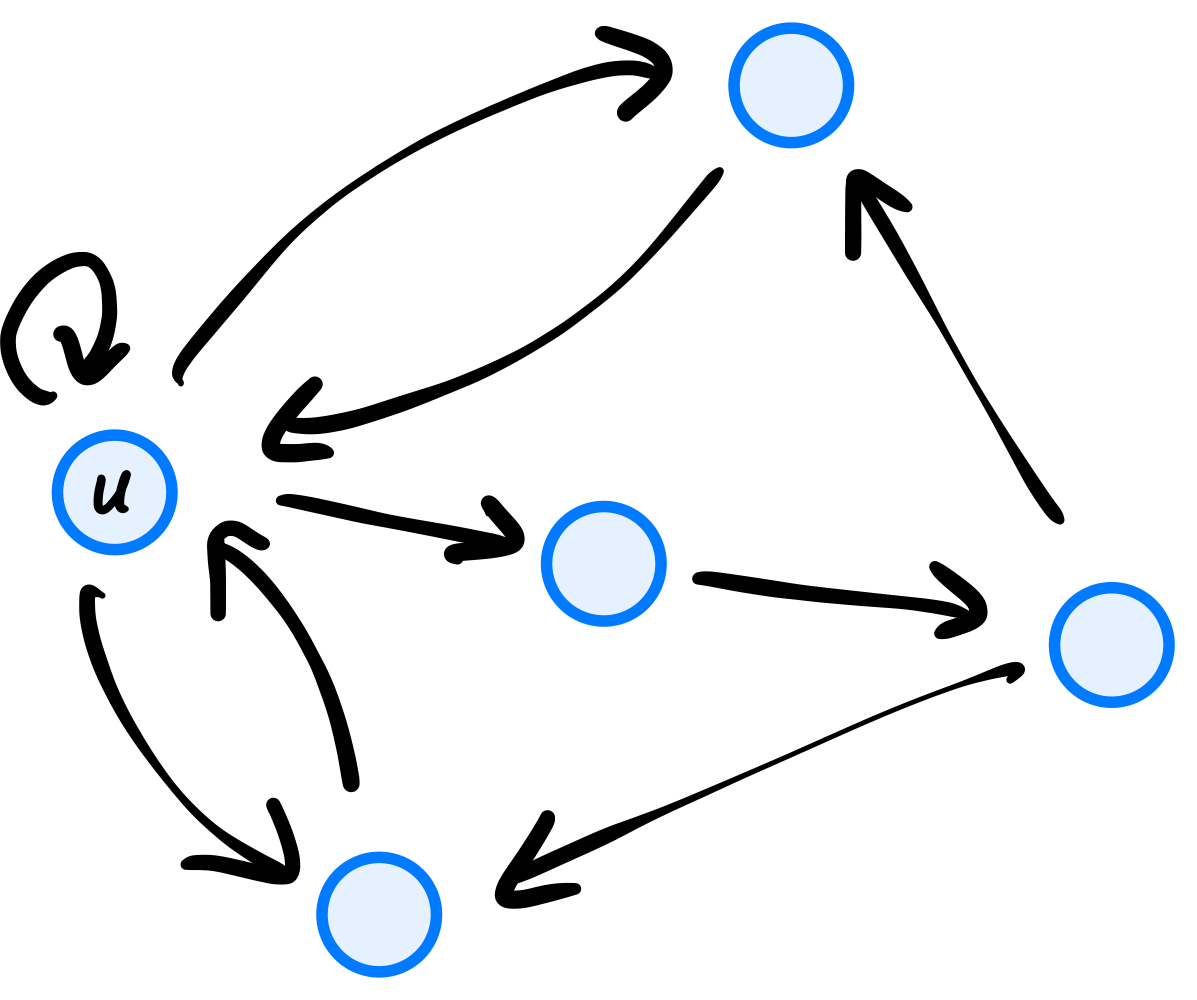
Solution
4
Problem #126
Tags: aggregate analysis, graph representations
Suppose a graph \(G = (V, E)\) is stored using an adjacency list representation in the variable adj_list. What is the time complexity of the below code?
for lst in adj_list:
for u in lst:
print(u)
Solution
\(\Theta(V + E)\)
Problem #127
Tags: breadth first search
Suppose a BFS is run on the graph below using node 1 as the source node. Which node will be the BFS predecessor of node 8? You should use the convention that neighbors are produced in ascending order by label.
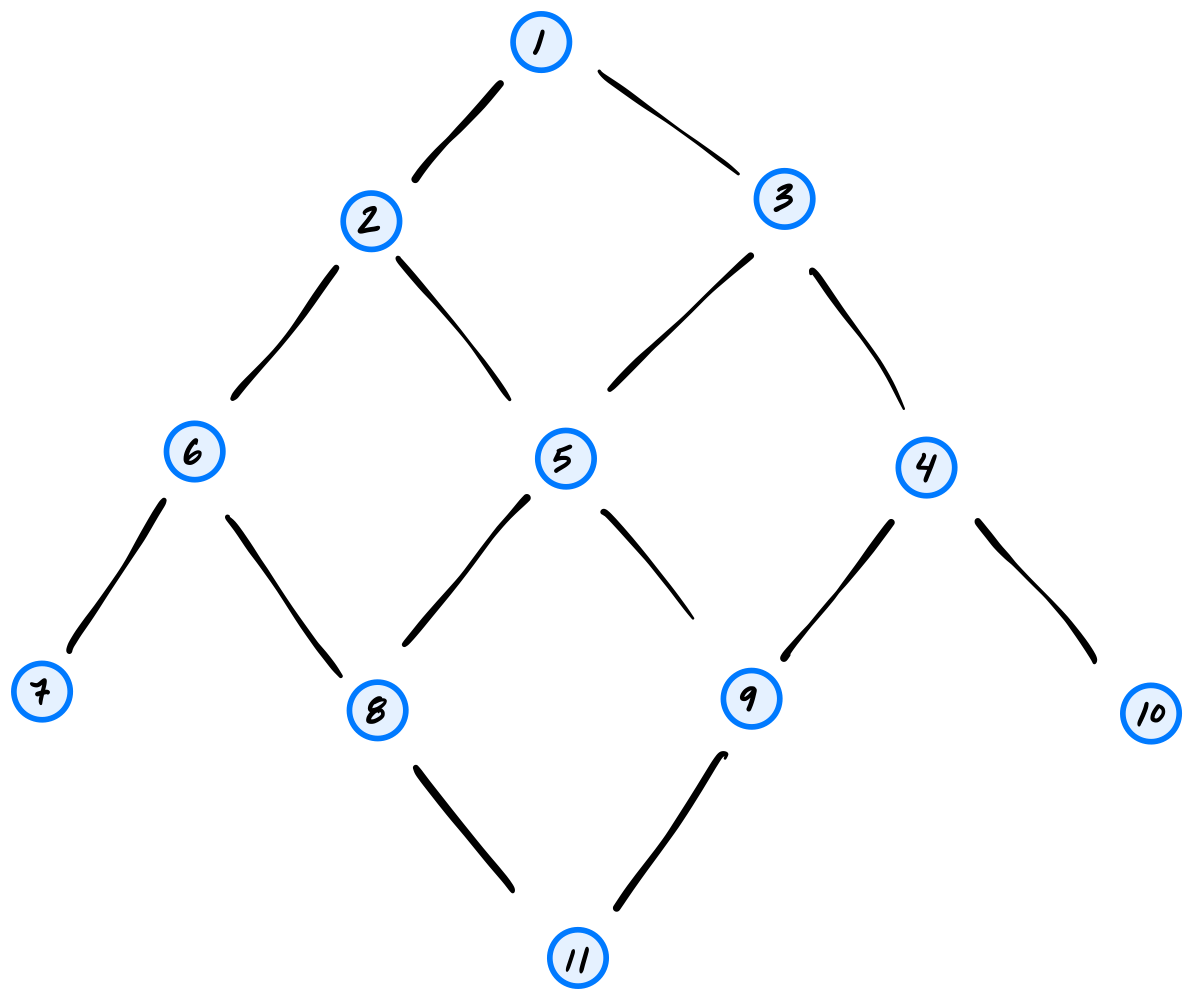
Solution
5
Problem #128
Tags: breadth first search
Suppose a ``2-chain'' graph with \(n\) nodes is constructed by taking \(n\) nodes labeled 1, 2, \(\ldots\), \(n\), and, for each node \(u\), making an edge to nodes \(u + 1\) and \(u + 2\)(if they are in the graph).
For example, such a graph with \(n = 7\) looks like:

Suppose BFS is run on a 2-chain graph with \(n\) nodes, using node 1 as the source. What is the time taken as a function of \(n\)? State your answer using asymptotic notation.
Solution
\(\Theta(n)\)
Problem #129
Tags: depth first search
Suppose a DFS is run on the graph shown below using node 11 as the source.
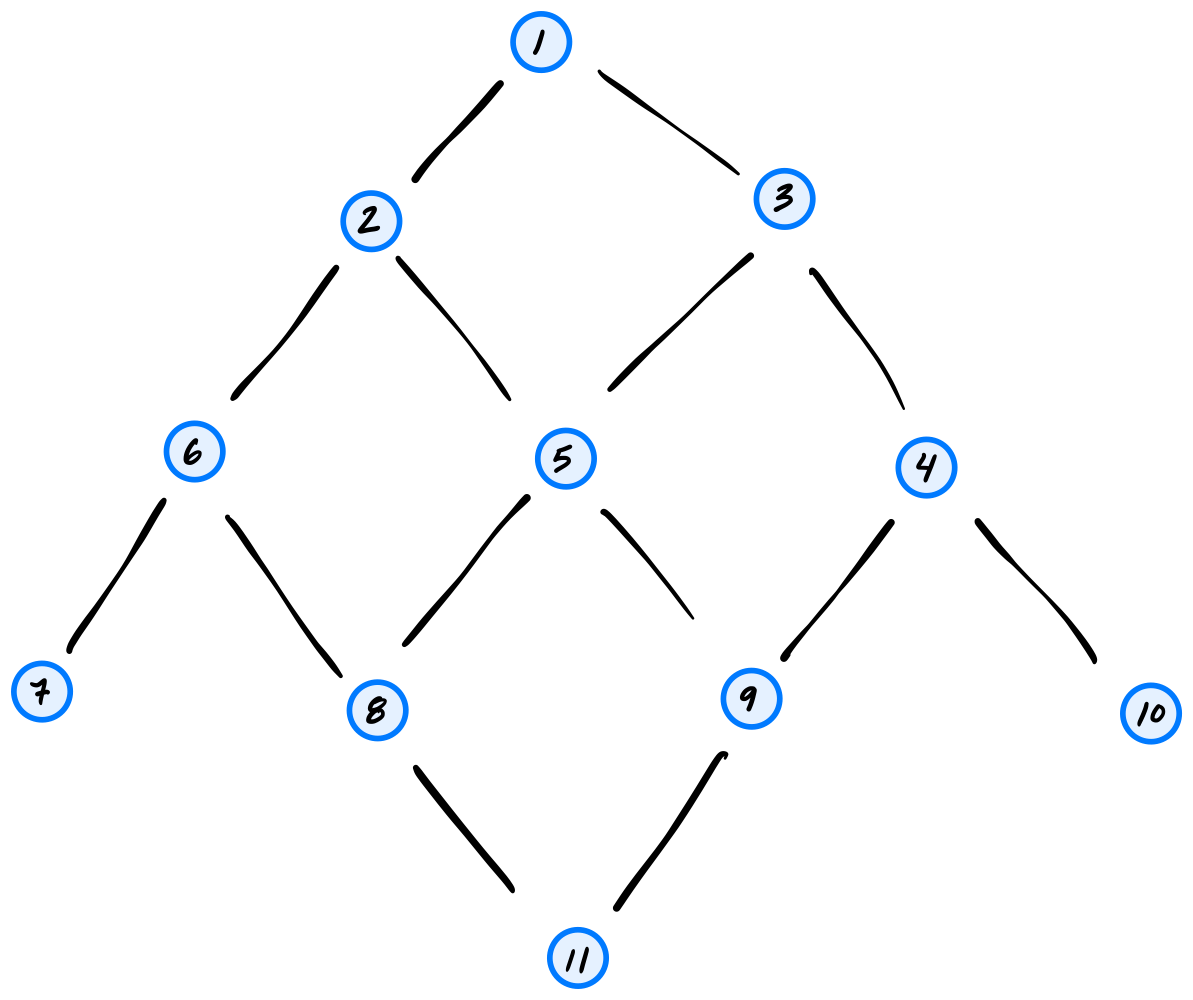
What will be the DFS predecessor of node 3 in the search? Use the convention that a node's neighbors are produced in ascending order by label.
Solution
1
Problem #130
Tags: depth first search, aggregate analysis
Consider the code shown below. It shows DFS as seen in lecture, with one modification: a print statement in the for-loop.
def dfs(graph, u, status=None):
"""Start a DFS at `u`."""
# initialize status if it was not passed
if status is None:
status = {node: 'undiscovered' for node in graph.nodes}
status[u] = 'pending'
for v in graph.neighbors(u):
print("Hello!")
if status[v] == 'undiscovered':
dfs(graph, v, status)
status[u] = 'visited'
How many times will "Hello!" be printed if dfs is run on the graph below using node \(u\) as the source? Note that dfs will not be restarted if the first call does not explore the whole graph.
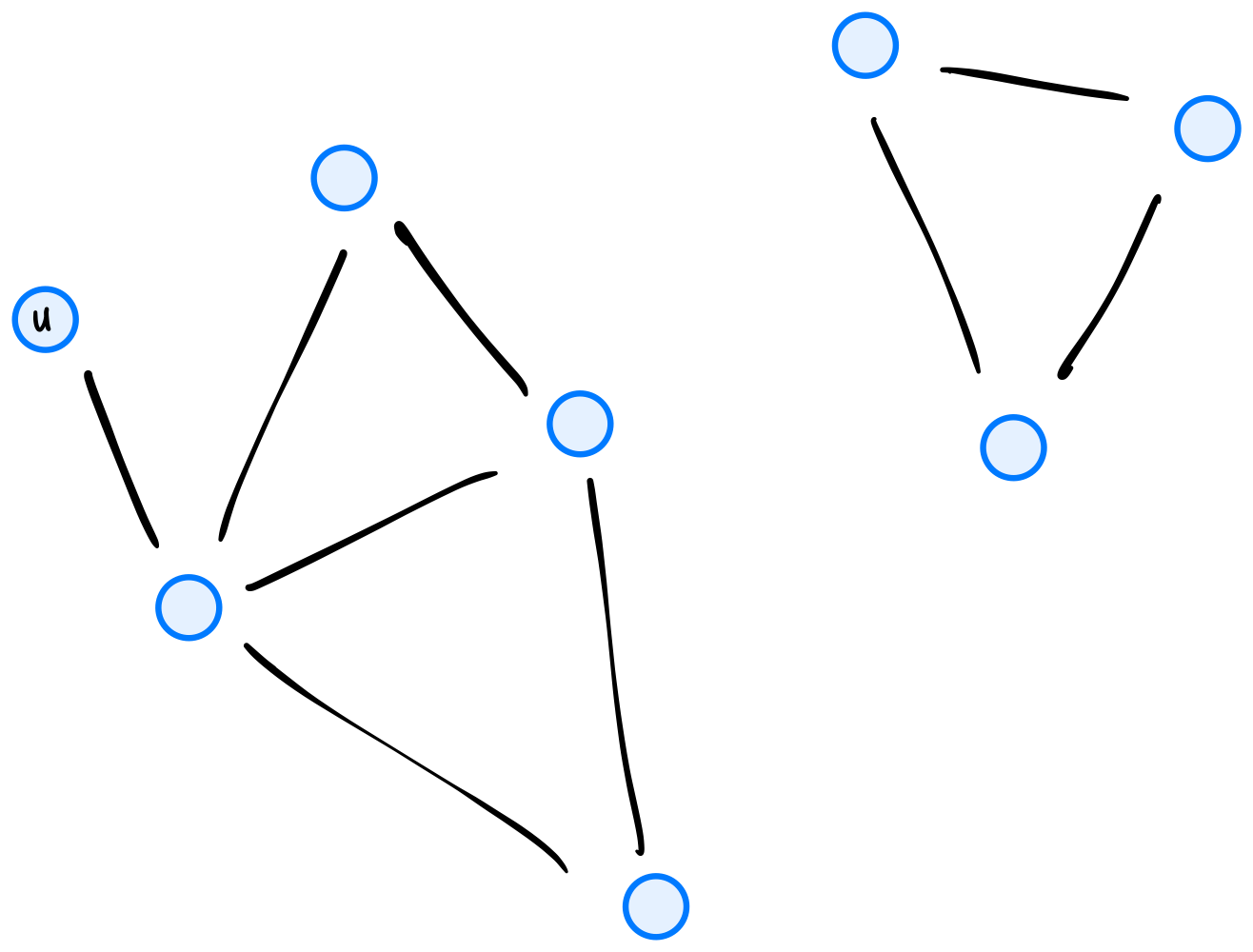
Solution
12
Problem #131
Tags: depth first search, start and finish times
Suppose again that a DFS is run on the graph shown in the above problem using node 11 as the source.
Part 1)
What will be the start time of node 2? Use the convention that the start time of the source is 1.
Solution
4
Part 2)
What will be the finish time of node 10?
Solution
11
Problem #132
Tags: depth first search, start and finish times
In a DFS on an undirected graph \(G\), the start time of node \(u\) is 12, while the finish time of node \(u\) is 37. How many nodes were marked pending between the moment that node \(u\) was marked pending and the moment that it was marked visited? Node \(u\) itself should be excluded from your count.
Solution
12
Problem #133
Tags: aggregate analysis
A ``hub and spoke'' graph with \(n\) nodes consists of a single ``hub'' node \(h\) along with \(n - 1\) ``spoke'' nodes, \(u_1, \ldots, u_{n-1}\) and \(n - 1\) edges from the hub node \(h\) to each of the spoke nodes. For example, a ``hub and spoke'' graph with 8 nodes looks like the below:
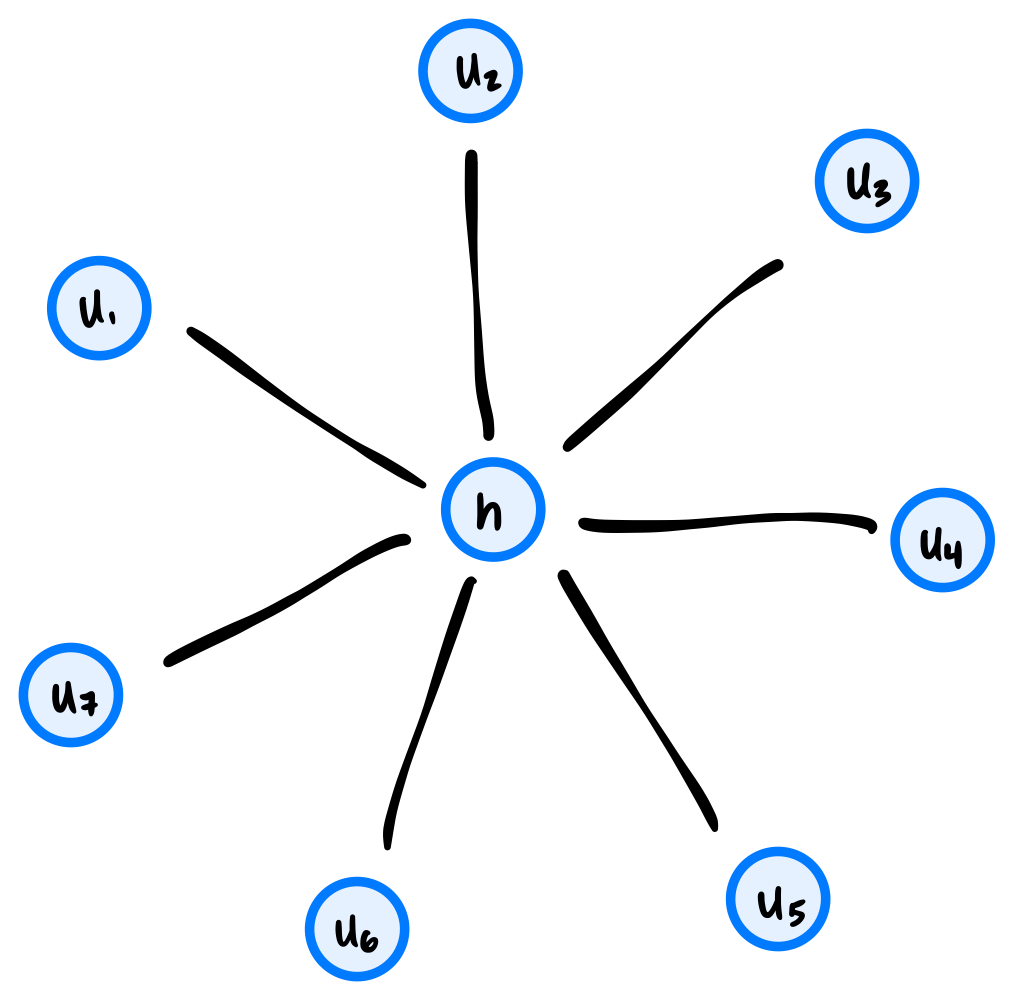
What is the worst case time complexity of an optimal algorithm which takes as input an arbitrary graph \(G = (V, E)\) and determines if it is a ``hub and spoke'' graph? You may assume that the graph is represented as an adjacency list and that the total number of edges in the graph can be retrieved in constant time.
Solution
\(\Theta(1)\) Here's the algorithm. First, check that the number of edges is \(|V| - 1\). If not, it's not a ``hub and spoke'' graph. This takes constant time, by the assumption that the total number of edges can be retrieved in constant time.
Next, take an arbitrary node and compute its degree (in \(\Theta(1)\) time), since the graph is represented as an adjacency list). If the degree is \(n - 1\), then the graph is a ``hub and spoke'' graph, and this is the hub.
If the degree is not \(n - 1\), but instead 1, this node might be a spoke. Check the degree of its neighbor as described above to see if its a hub.
If you see a degree that's neither 1 nor \(n - 1\), then the graph is not a ``hub and spoke'' graph.
Problem #134
Tags: bellman-ford
Suppose the Bellman-Ford algorithm with early stopping is run on the weighted graph shown below using node \(s\) as the source (the edge weights are intentionally not shown). In the worst case, how many iterations of Bellman-Ford will be performed? That is, how many iterations of the outer for-loop will occur?
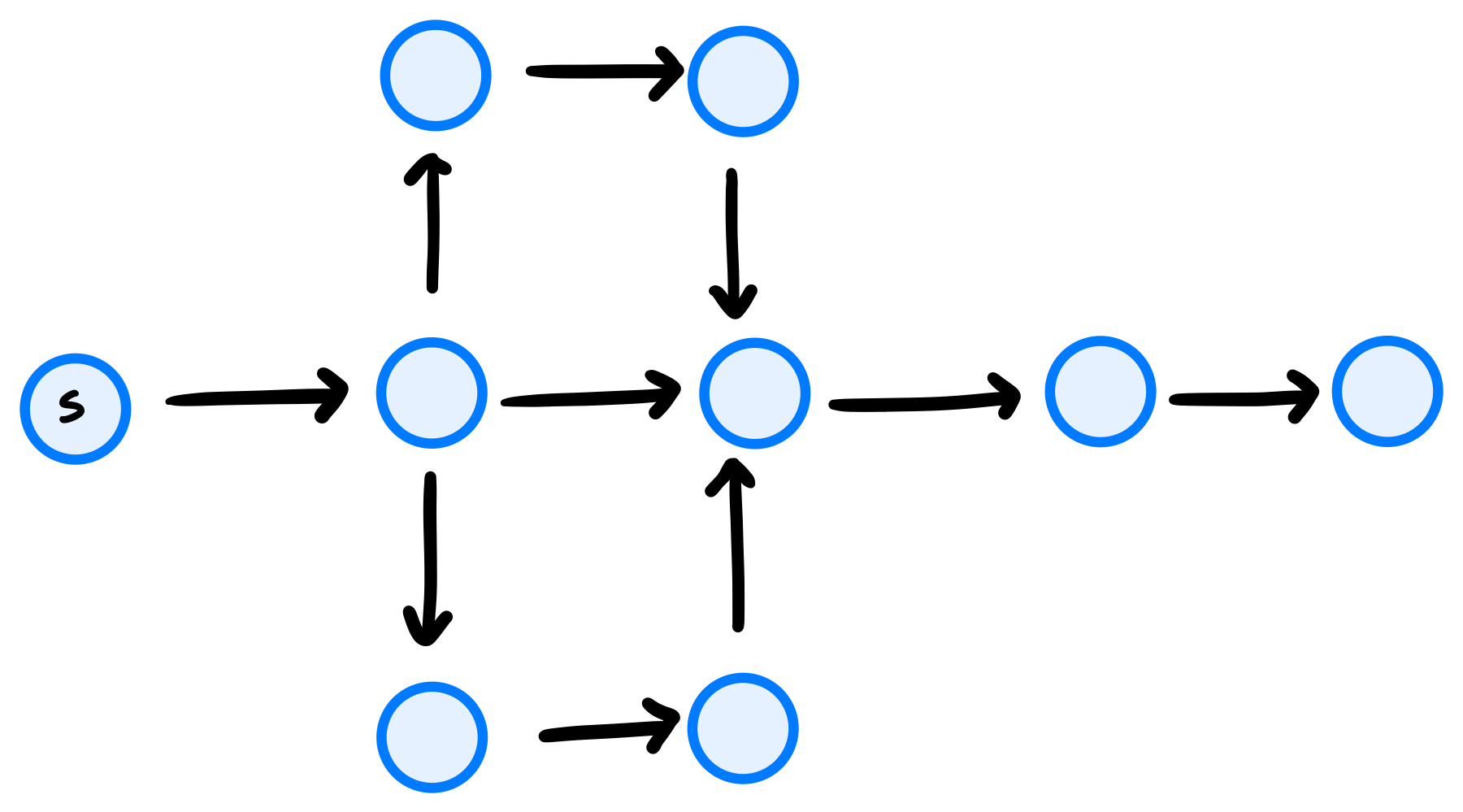
Solution
7
Problem #135
Tags: bellman-ford
Again consider a ``2-chain'' graph, which was defined above to the a graph with \(n\) nodes that is constructed by taking \(n\) nodes labeled 1, 2, \(\ldots\), \(n\), and, for each node \(u\), making an edge to nodes \(u + 1\) and \(u + 2\)(if they are in the graph).
Suppose the Bellman-Ford algorithm without early stopping is run on a 2-chain graph with \(n\) nodes, using node 1 as the source. What is the time taken as a function of \(n\)? State your answer using asymptotic notation.
Solution
\(\Theta(n^2)\)
Problem #136
Tags: depth first search, breadth first search
Suppose both BFS and DFS are run on the same graph \(G = (V, E)\) using the same source node. Assume that \(G\) is a tree. Consider a particular node \(u\) in the graph. True or False: the BFS predecessor found for \(u\) and the DFS predecessor found for \(u\) must be the same.
Solution
True.
Problem #137
Tags: depth first search
Suppose a DFS is run on a directed graph. Let \(u\) and \(v\) be two nodes in the graph, and assume that the edge \((u, v)\) exists. True or False: it is possible that, at some moment in time, \(u\) is marked as ``visited'' while \(v\) is marked as ``undiscovered''.
Solution
False.
Problem #139
Tags: graph representations
Let \(A\) be the adjacency matrix of the graph shown below:
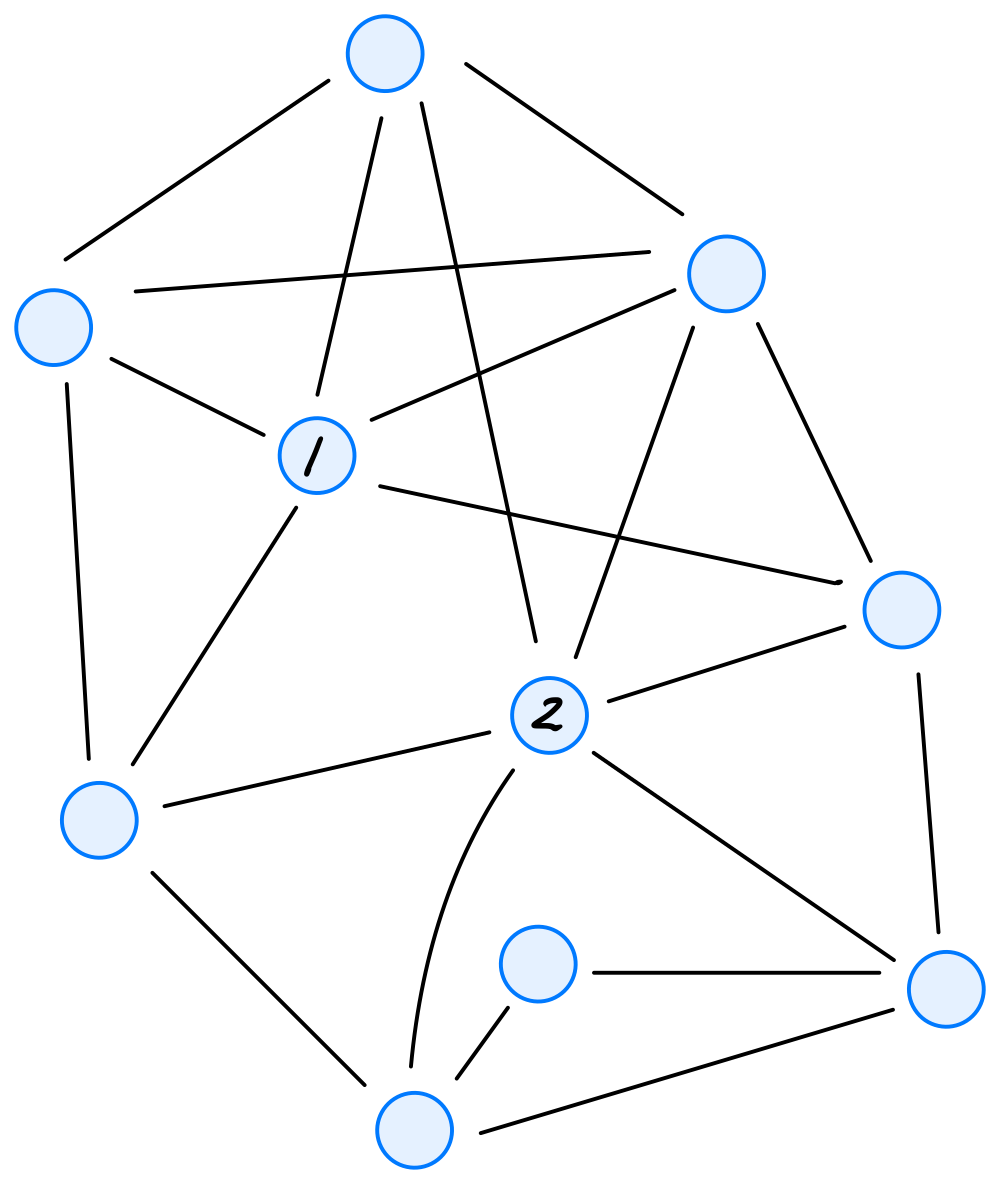
Let \(\vec{a}^{(1)}\) be the first row of \(A\) and \(\vec{a}^{(2)}\) be the second row of \(A\). What is \(\vec{a}^{(1)}\cdot\vec{a}^{(2)}\)? That is, what is the dot product between the first row of \(A\) and the second row of \(A\)? Your answer should be in the form of a number.
It may help to recall that the dot product between vectors \(\vec x = (x_1, \ldots, x_d)^T\) and \(\vec y = (y_1, \ldots, y_d)^T\) is equal to \(x_1 y_1 + x_2 y_2 + \ldots + x_d y_d\).
Solution
4
Problem #140
Tags: hashing
Suppose \(T\) is a hash table of size 100 (that is, it has 100 bins). 300 elements are inserted into the hash table using a hash function that satisfies the uniform hashing assumption (that is, any element is equally-likely to hash into any bin). What is the expected number of elements in the first bin?
Solution
3
Problem #141
Tags: hashing
Suppose a hash table is constructed using linked lists to store the data within each bin, and that collisions are resolved by chaining. What is the worst case time complexity of inserting a new element into the hash table? You may assume that the hash table will not need to be resized, and that evaluating the hash function takes \(\Theta(1)\) time.
Solution
\(\Theta(1)\). Inserting an item into a hash table takes two steps: first, we hash the item to find its bin -- this takes \(\Theta(1)\) time. Next, we actually insert the item into that bin. When we use chaining, we do this by appending the item to the linked list containing that bins elements. Appending to a linked list takes \(\Theta(1)\) time, and so overall this takes \(\Theta(1)\).
Problem #142
Tags: graph theory
Suppose \(u\) is a node in a complete, undirected graph \(G = (V,E)\). What is the degree of \(u\)? Remember, an undirected graph is complete if it contains every possible edge.
Solution
\(|V| - 1\)
Problem #143
Tags: graph theory
Let \(V = \{a, b, c, d\}\) and \(E = \{(a,b), (a,a), (a,c), (d,b), (c,a)\}\) be the nodes and edges of a directed graph. How many predecessors does node \(b\) have?
Solution
2
Problem #144
Tags: connected components, graph theory
Let \(C\) be a connected component in an undirected graph \(G\). Suppose \(u_1\) is a node in \(C\) and let \(u_2\) be a node that is reachable from \(u_1\). True or False: \(u_2\) must also be in the same connected component, \(C\).
Solution
True.
Problem #145
Tags: graph representations
Let \(A\) be the adjacency matrix representing a directed graph with $n$ nodes. What is the greatest possible sum of any row of \(A\)?
Solution
\(n\)
Problem #146
Tags: graph theory
Let \(G = (V, E)\) be a connected, undirected graph with 16 nodes and 35 edges. What is the greatest possible number of edges that can be in a simple path within \(G\)?
Solution
15
Problem #147
Tags: connected components, graph theory
Suppose \(G = (V, E)\) is an undirected graph. Let \(k\) be the number of connected components in \(G\). True or False: it is possible that \(k > |E|\).
Solution
True.
Problem #148
Tags: graph theory
Let \(G = (V, E)\) be a directed graph, and suppose \(u, v, w \in V\) are all nodes. True or False: if \(w\) is reachable from \(v\), and \(v\) is reachable from \(u\), then \(w\) is reachable from \(u\).
Solution
True.
Problem #149
Tags: graph theory
Let \(G = (V,E)\) be a connected, undirected graph with \(|E| = |V| - 1\). Suppose \(u\) and \(v\) are both nodes in \(G\). True or False: there can be more than one simple path from \(u\) to \(v\).
Solution
False.
Problem #150
Tags: connected components, graph theory
Suppose an undirected graph \(G = (V,E)\) has two connected components, \(C_1\) and \(C_2\). Suppose that \(|C_1| = 4\) and \(|C_2| = 3\). What is the largest that \(|E|\) can possibly be?
Solution
Answer: 9. To load a graph with the most edges, make each connected component "fully connected". The most edges we can put in a component with 4 nodes is \(4 * 3 / 2 = 6\), and the most we can put into a component with 3 nodes is \(3 * 2 / 2 = 3\). Therefore, we can put at most 9 edges in this graph.
Problem #151
Tags: breadth first search
Suppose a breadth first search (BFS) is run on the graph shown below using node \(u_4\) as the source and the convention that graph.neighbors produces nodes in ascending order by label. What will be the predecessor of \(u_6\) in the BFS?

Solution
\(u_2\)
Problem #152
Tags: depth first search
Suppose a depth first search (DFS) is run on the graph shown below using node \(u_4\) as the source and the convention that graph.neighbors produces nodes in ascending order by label. What will be the predecessor of \(u_6\) in the DFS?

Solution
\(u_5\). DFS starts at \(u_4\), looks at the neighbors, and sees \(u_2\) is undiscovered, so it makes a recursive call dfs(u_2). At \(u_2\), it sees that \(u_1\) is undiscovered, and calls dfs(u_1). At \(u_1\), there's nothing to do, so it's marked as visited and the recursion unrolls back to the call on dfs(u_2). We then look at the next neighbor of \(u_2\), which is \(u_3\). We make a call to dfs(u_3), which looks at its neighbors and sees \(u_5\). We make a call to dfs(u_5), and during this call we discover \(u_6\), meaning that \(u_5\) is the DFS predecessor of \(u_6\).
Problem #153
Tags: breadth first search
Suppose a breadth first search (BFS) is run on a graph \(G = (V, E)\), and that node \(u\) is distance 5 from the source while node \(v\) is distance 3 from the source. True or False: it is possible that at some point during the BFS, both \(u\) and \(v\) are in the pending queue at the same time.
Solution
False.
Problem #154
Tags: aggregate analysis
Suppose the code below is run on a graph \(G = (V, E)\). What is its time complexity? You may assume that \(|E| \geq 1\).
for u in graph.nodes:
for v in graph.neighbors(u):
print(u, v)
Solution
\(\Theta(V + E)\)
Problem #156
Tags: depth first search, trees
What is the time complexity of depth first search (DFS) when run on a tree with \(n\) nodes?
Solution
\(\Theta(n)\)
Problem #157
Tags: depth first search
Suppose a depth first search is run on a directed graph. True or False: it is possible that, at any moment in time, there is a node marked as visited which has a neighbor (successor) that is marked as pending.
Solution
True
Problem #158
Tags: depth first search, start and finish times
Suppose a depth first search is run on the graph shown below using node \(u_4\) as the source, and adopt the convention that graph.neighbors produces nodes in ascending order of label. Which node will have the smallest finish time?

Solution
\(u_1\)
Problem #159
Tags: depth first search, start and finish times
Suppose a depth first search is run on the graph shown below using node \(u_4\) as the source, and adopt the convention that graph.neighbors produces nodes in ascending order of label. What will be the start time of node \(u_7\)?

Solution
12
Problem #160
Tags: topological sorting
Let \(G = (V,E)\) be the directed graph with \(V = \{a, b, c, d, e\}\) and \(E = \{(a, b), (a, c), (a, d), (b, e), (c, e), (d, e)\}\). How many valid topological sorts of $V$ are there?
Solution
6
Problem #161
Tags: depth first search, start and finish times
Suppose \(T = (V, E)\) is a connected, undirected graph with no cycles (that is, \(T\) is a tree). Suppose a depth first search is run on \(T\) using node s as the source. Assume that node s has two neighbors: \(u\) and \(v\). If \(|V| = 15\), which one of the below represents possible start and finish times of \(u\) and \(v\)? You may assume that graph.neighbors produces neighbors in ascending order of label.
Solution
start[u] = 2, finish[u] = 21, start[v] = 22, finish[v] = 29
Problem #163
Tags: bellman-ford
Recall that Bellman-Ford with early stopping updates edges iteratively until no estimated distances change, at which point the algorithm terminates early. True or False: the number of iterations needed before early termination may depend on the order in which the edges are updated.
Solution
True
Problem #164
Tags: breadth first search
Suppose that every edge in the weighted graph \(G\) has weight -5. True or False: breadth first search on this graph will compute a longest path from the source to every node in the graph (that is, a path with greatest possible total edge weight).
You may assume that every node in the graph is reachable from the source.
Solution
True
Problem #209
Tags: graph theory
Suppose an undirected graph has 16 edges. What is the smallest number of nodes it can have?
Problem #210
Tags: graph theory
Suppose a directed graph has 5 nodes and 3 edges. What is the greatest possible degree of any node in the graph?
Solution
Remember that nodes can have self loops, and that the degree of a node with only a self-loop is 2. So a node that has a self loop and two other edges leaving it has a degree of 4.
Problem #211
Tags: connected components
Let \(G = (V,E)\) be an undirected graph with:
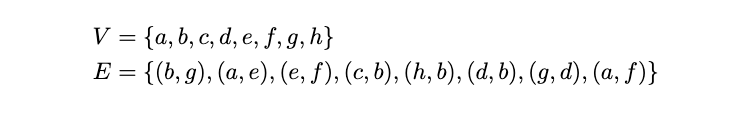
True or False: \(\{b, d, g\}\) is a connected component of this graph.
Solution
False. The connected components of this graph are \(\{a, e, f\}\) and \(\{b, c, d, g, h\}\).
Remember: a connected component has to contain all nodes reachable from any node in the component. While \(b\), \(d\), and \(g\) are all reachable from one another (and are ``connected''), they do not form a connected component because there are more nodes reachable from this group: namely, \(h\) and \(c\).
Problem #212
Tags: hashing
In the problem below, suppose arr is an array of \(n\) integers. What is the expected time complexity of the code below? Write your answer using asymptotic notation as a function of \(n\).
Remember: set is implemented using a hash table. You may assume that the hash table is large enough to store all of th numbers without needing to resize.
def find_duplicates(arr):
seen = set()
duplicates = set()
for num in arr:
if num in seen:
duplicates.add(num)
else:
seen.add(num)
return duplicates
Problem #213
Tags: depth first search
A modification of the dfs function from lecture is shown below. It is the same as the original dfs function, except that it has an added print statement.
def dfs(graph, u, status=None):
"""Start a DFS at `u`."""
# initialize status if it was not passed
if status is None:
status = {node: 'undiscovered' for node in graph.nodes}
status[u] = 'pending'
for v in graph.neighbors(u):
print("Hello!")
if status[v] == 'undiscovered':
dfs(graph, v, status)
status[u] = 'visited'
Consider running this algorithm on the following graph, starting at node \(a\):
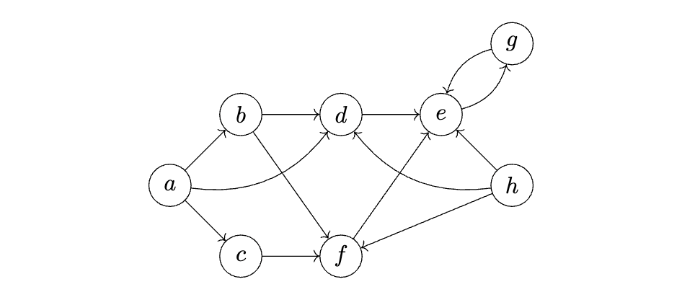
How many times will "Hello!" be printed? Note that this is not a full DFS, and that not all nodes are reachable from \(a\).
Problem #214
Tags: depth first search
True or False: a depth first search with source node \(s\) is guaranteed to find the longest simple path starting from \(s\) in a connected, undirected graph \(G\) That is, suppose that there is a unique longest simple path in \(G\), and call this path \(p\). True or False: the longest simple path in the DFS forest must be also be \(p\).
Solution
False
Problem #215
Tags: breadth first search
Suppose a breadth first search on an undirected, connected graph is paused at a particular moment in time and the node statuses are printed. Suppose it is found that all nodes which are distance 6 from the source are marked ``visited''.
True or False: it is possible that there is a node, distance 7 from the source, whose status is ``undiscovered''.
Solution
False
Problem #216
Tags: depth first search
Suppose a depth first search (DFS) is run on the graph below, starting at node \(a\). Start and finish times are calculated using the convention that the start time of node \(a\) is 1.
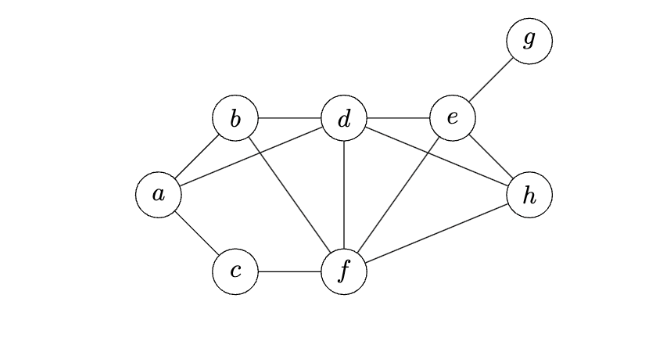
What will be the finish time of node \(e\)? Assume the convention that a node's neighbors are produced in alphabetical order.
Problem #217
Tags: depth first search
Suppose that a depth first search is being performed on an undirected graph, and when dfs is called on a node \(u\), the statuses of all of its neighbors are printed. True or False: it is possible that one of the neighbors is marked as ``visited''.
Solution
False
Problem #218
Tags: breadth first search
Suppose a breadth first search (BFS) is performed on the graph shown below using node \(a\) as the source. Which node will be the BFS predecessor of node \(h\) when the search is complete? You should use the convention that neighbors are produced in alphabetical order.
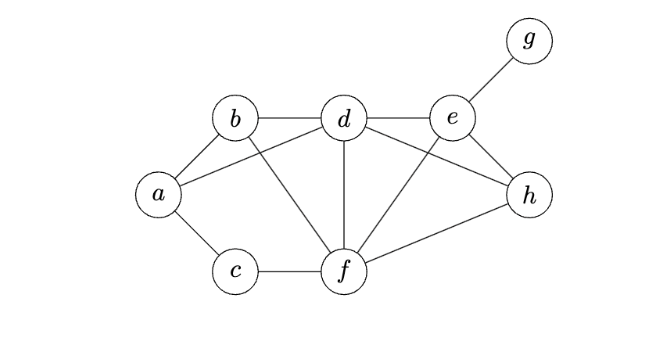
Problem #219
Tags: start and finish times
Suppose an undirected graph has 50 nodes. A full DFS is run on the graph to compute start and finish times. Suppose that, for each node, the difference between the node's start and finish is printed, and the largest difference is found to be 15.
True or False: it is possible that the graph is connected.
Solution
False
Problem #221
Tags: connected components
Let \(G\) be an undirected graph, and suppose \(u\) and \(v\) are two nodes belonging to the same connected component of \(G\), with \(v\) being a neighbor of \(u\). That is, the edge \((u, v)\) is in \(G\).
Let \(G'\) be the graph obtained from \(G\) by deleting the edge \((u, v)\). True or False: \(u\) and \(v\) must still be in the same connected component of the new graph, \(G'\).
Solution
False
Problem #222
Tags: graph representations
An ``isolated node'' in a graph is a node that has no edges attached to it.
What is the worst case time complexity of an efficient algorithm that checks to see if a graph \(G = (V, E)\) has an isolated node? You should assume that the graph is represented as an adjacency list.
Solution
\(\Theta(V)\)
Problem #223
Tags: graph theory
The adjacency matrix of a directed graph with nodes \(u_1, \ldots, u_8\) is shown below:
True or False: there is a path from node \(u_1\) to node \(u_8\).
Solution
True
Problem #224
Tags: hashing
Assume that a hash table is implemented using chaining to resolve collisions. The hash table stores \(n\) numbers.
Suppose a membership query is made for 42. True or False: more than one bin in the hash table may be checked with a linear search during the query.
Solution
False
Problem #225
Tags: graph theory
Let \(G = (V, E)\) be a directed graph with the property that there is a node \(u\) in \(G\) such that every other node in \(G\) is reachable from \(u\).
Let \(H \) be the directed graph obtained from \(G\) by reversing the direction of every edge. True or False: there must be a node \(v\) in \(H\) such that every other node in \(H\) is reachable from \(v\).
Solution
False. Consider the graph \(a \leftarrow b \rightarrow c\). Every node is reachable from \(b\). Now flip the edges to get the graph: \(a \rightarrow b \leftarrow c\). There's no node from which every other node is reachable.
Problem #226
Tags: dijkstra
Suppose Dijkstra's algorithm is run on the graph shown below using node \(a\) as the source.
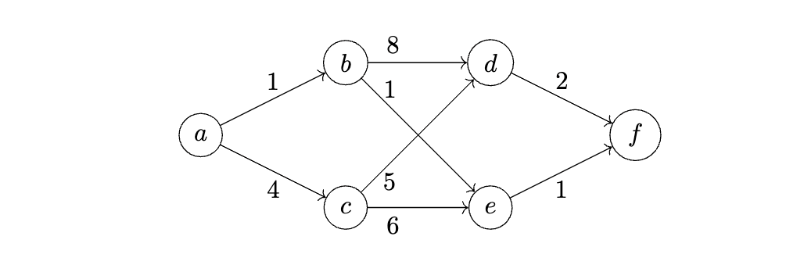
What will be the fourth node popped from the priority queue? (The first node popped is the source, \(a\).)
Problem #227
Tags: bellman-ford
Suppose Bellman-Ford with early stopping is run on the weighted graph below whose edge weights are unknown to us (but known to the algorithm). The algorithm uses node \(a\) as the source node.
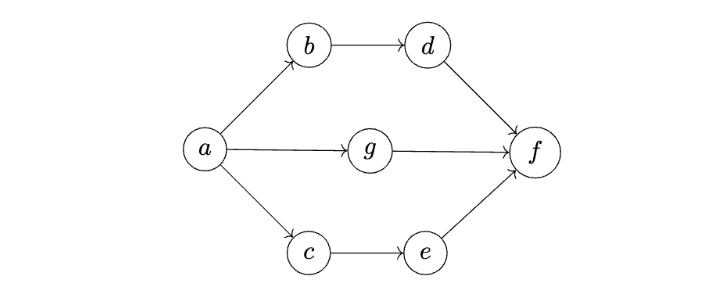
How many iterations of the outer loop will be run in the worst case? Your answer should be a number.
Problem #228
Tags: breadth first search
Consider the following modification of BFS, with an added print statement:
from collections import deque
def modified_bfs(graph, source):
"""Start a BFS at `source`."""
status = {node: 'undiscovered' for node in graph.nodes}
status[source] = 'pending'
pending = deque([source])
while pending:
u = pending.popleft()
for v in graph.neighbors(u):
if v == 9:
print("Here!") # <-- this is the added print statement
if status[v] == 'undiscovered':
status[v] = 'pending'
pending.append(v)
status[u] = 'visited'
Consider running this algorithm on the following graph, starting at node \(1\):
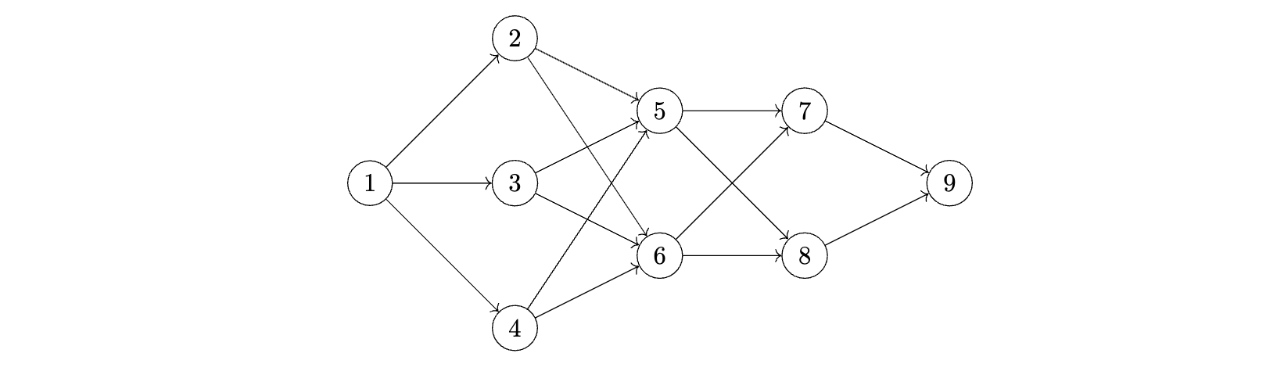
How many times will "Here!" be printed?
Problem #229
Tags: breadth first search
Suppose a breadth-first search is performed on the following tree, starting at the root node \(s\):
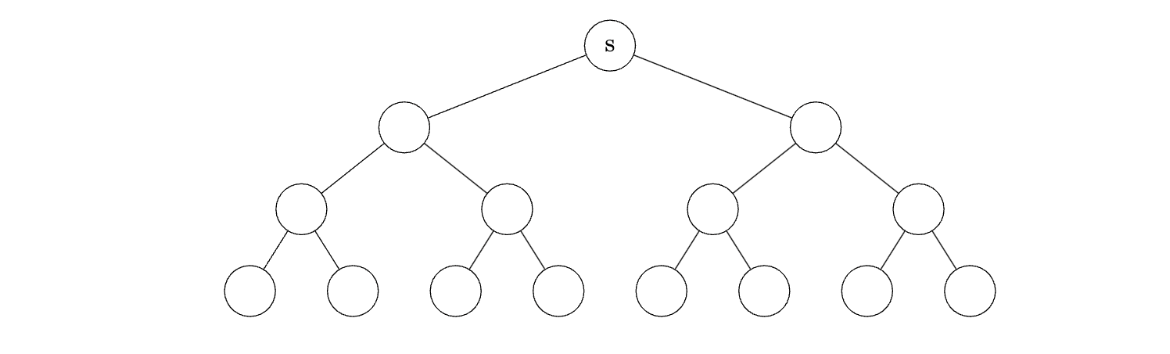
What is the most number of nodes that can be in the queue at any one time?
Problem #230
Tags: breadth first search
Consider the code below, which is a modification of the BFS algorithm presented in lecture: there are two new lines, marked with comments.
from collections import deque
def modified_bfs(graph, source):
"""Start a BFS at `source`."""
status = {node: 'undiscovered' for node in graph.nodes}
status[source] = 'pending'
pending = deque([source])
while pending:
u = pending.popleft()
for v in graph.neighbors(u):
for node in graph.nodes: # < -- this is the modification
print(status[node]) # < -- this is the modification
if status[v] == 'undiscovered':
status[v] = 'pending'
pending.append(v)
status[u] = 'visited'
What is the time complexity of this algorithm, in terms of \(|V|\) and \(|E|\)? You may assume the graph is undirected and connected, so that all nodes are reachable from the source.
Solution
Because the graph is connected, \(|E| \geq |V| - 1\), and so \(\Theta(VE)\) and \(\Theta(VE + V)\) are equivalent. Only \(\Theta(VE + V)\) is an option so \(\Theta(VE + V)\) is the correct answer.
Problem #231
Tags: shortest path, graph theory
Suppose an undirected, connected graph has \(n\) nodes, half of which are colored red and the other half are colored blue. Each red node is neighbors with \(n/4\) blue nodes, and each blue node is neighbors with \(n/4\) red nodes. There are no edges between nodes of the same color.
What is the time complexity of computing a shortest path from a given red node to all other red nodes using BFS?
Solution
\(\Theta(n^2)\)
Problem #232
Tags: bellman-ford
Suppose the Bellman-Ford algorithm is run on the following graph using node \(a\) as the source node:
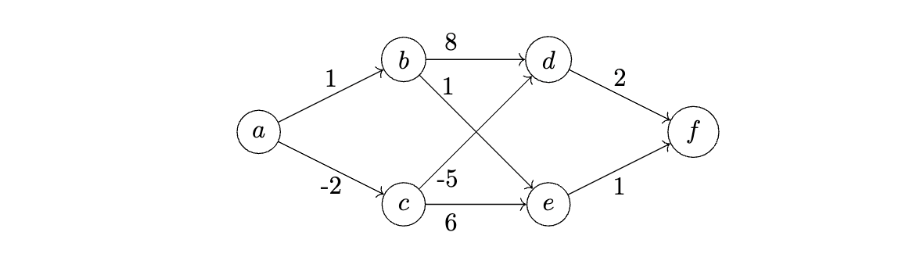
Suppose when graph.edges is called, the edges are returned in the order:
\((a, b), (c, e), (d, f), (c, d), (b, d), (b, e), (a, c), (e, f) \).
After one iteration of the outer loop of Bellman-Ford, what is the estimated distance to node \(d\)?
Problem #233
Tags: connected components
Let \(G = (V,E)\) be an undirected graph with:
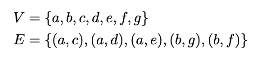
True or False: \(\{a, d, e\}\) is a connected component of this graph.
Solution
False
Problem #234
Tags: graph theory
Let \(G = (V, E)\) be a connected, undirected graph with \(|E| = |V| - 1\). Suppose \(u\) and \(v\) are two nodes in \(V\).
True or False: there can be two different simple paths from \(u\) to \(v\) in \(G\).
Solution
False
Problem #235
Tags: connected components
Suppose that every node in an undirected graph with \(n\) nodes has degree 2.
True or False: \(G\) must have one connected component.
Solution
False
Problem #236
Tags: connected components
Suppose an undirected graph has 3 connected components and 7 nodes. What is the maximum number of edges it can have?
Problem #237
Tags: dijkstra
Suppose Dijkstra's algorithm is run on the graph shown below using node \(a\) as the source.
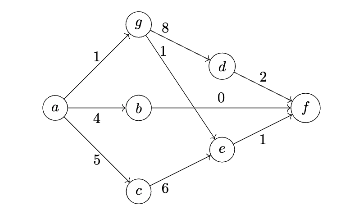
Suppose \(C\) is the set of ``correct'' nodes: that is, \(C\) is the set of nodes whose estimated distances are known to be correct.
What will be the fifth node added to \(C\) by Dijkstra's algorithm? (The first node added to \(C\) is the source, \(a\).)
Problem #238
Tags: depth first search
A modification of the dfs function from lecture is shown below. It is the same as the original dfs function, except that it has an added print statement.
def dfs(graph, u, status=None):
"""Start a DFS at `u`."""
# initialize status if it was not passed
if status is None:
status = {node: 'undiscovered' for node in graph.nodes}
status[u] = 'pending'
for v in graph.neighbors(u):
if status[v] == 'undiscovered':
print("Hello!")
dfs(graph, v, status)
status[u] = 'visited'
Consider running this algorithm on the following graph, starting at node \(a\):
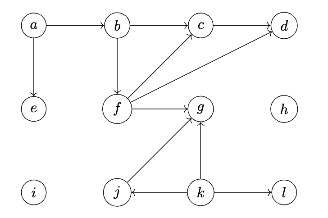
How many times will "Hello!" be printed? Note that this is not a full DFS, and that not all nodes are reachable from \(a\).
Problem #239
Tags: breadth first search
The table below shows the number of nodes in a graph \(G\) which are distance 0 from node \(s\), distance 1 from node \(s\), distance 2, etc.:
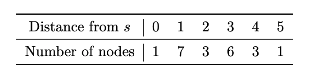
Suppose a BFS is performed on this graph with node \(s\) as the starting node. What is the largest number of nodes that could possibly be in the queue at any one time?
Solution
Remember that the queue can only simultaneously contain nodes at two different distances (it can't contain nodes at distance 1, distance 2, and distance 3 at the same time, but it can contain nodes at distance 1 and distance 2 at the same time).
The largest number of nodes that could possibly be in the queue at any one time is when we have (almost) all of the nodes from the first distance, and all of the nodes from the second distance.
In this graph, let \(u\) be a neighbor of the source, and suppose it has an edge with all nodes that are distance 2 from the source. If \(u\) is the first node popped from the queue (after the source), then once its neighbors are added to the queue, the queue will contain all of the nodes at distance 1 except for \(u\)(for 6 nodes in total), and all of the nodes at distance 2 (for 3 nodes in total). This gives us a total of 9 nodes in the queue.
Problem #240
Tags: depth first search
Suppose that a depth first search is being performed on an undirected graph, and when dfs is called on a node \(u\), the statuses of all of its neighbors are printed. True or False: it is possible that one of the neighbors is marked as ``visited''.
Solution
False
Problem #241
Tags: topological sorting
Suppose \(G\) is an acyclic directed graph. Let \(a\) and \(b\) be two nodes of \(G\) such that \(a\) appears before \(b\) in every possible topological sort of \(G\).
True or False: there must be a path from \(a\) to \(b\).
Solution
True
Problem #242
Tags: breadth first search
Suppose a BFS is run on the graph below using node 1 as the source node. Which node will be the BFS predecessor of node 9? You should use the convention that neighbors are produced in ascending order by label.
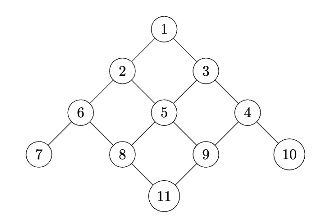
Problem #243
Tags: bellman-ford
Suppose Bellman-Ford with early stopping is run on the weighted graph below. The algorithm uses node \(a\) as the source node.
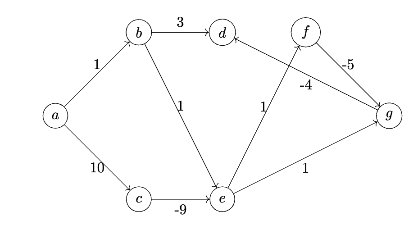
After the third iteration, name all nodes whose shortest path from \(a\) are guaranteed to be estimated correctly.
Solution
1st option: \(\{a,b,c,e,f\}\)
Problem #244
Tags: graph theory
Let \(G=(V,E)\) be an undirected graph with \(V=\{a,b,c,d,e\}\) and \(E=\{(a,b),(c,d),(e,a),(b,c),(e,d),(d,a)\}\).
True or False: it is possible to color nodes of \(G\) with red and blue such that there are no edges between nodes of the same color.
Solution
False
Problem #245
Tags: aggregate analysis
Suppose a graph \(G = (V, E)\) is stored using an adjacency list representation in the variable adj_list. What is the time complexity of the below code?
for u, lst in enumerate(adj_list):
for v in lst:
print(u, v, "is an edge")
Solution
2nd option: \(\Theta(V + E)\)
Problem #246
Tags: graph theory
A ``hub node'' in a graph is a node that has an edge to all the other nodes in the graph.
What is the worst case time complexity of an efficient algorithm that checks to see if a graph \(G = (V,E)\) has a hub node? You should assume that the graph is represented as an adjacency list. State your answer in asymptotic notation and in terms of \(V\) and \(E\).
Note: in studying, you might have come across a problem in the practice bank about ``hub and spoke'' graphs. This question is related, but not the same!
Problem #247
Tags: hashing
What is the expected time complexity of the code shown below? Assume that \(n\) is the length of the list of numbers, and write your answer in asymptotic notation in terms of \(n\).
def foo(numbers):
"""Assume that `numbers` is a list containing n numbers."""
# counts is a Python dictionary, which is implemented using a hash table
counts = {}
for x in numbers:
for y in numbers:
diff = abs(x - y)
if diff not in counts:
counts[diff] = 1
else:
counts[diff] = counts[diff] + 1
return counts
Problem #248
Tags: connected components
Let \(G = (V, E)\) be an undirected graph, and suppose that \(u, v, \) and \(w\) are three nodes in \(V\). Suppose that \(u\) and \(v\) are in the same connected component, but \(u\) and \(w\) are not in the same connected component. True or False: it is possible that \(v\) and \(w\) are in the same connected component.
Solution
False
Problem #249
Tags: depth first search
Suppose a depth first search (DFS) is run on the graph below, starting at node \(a\). Start and finish times are calculated using the convention that the start time of node \(a\) is 1.
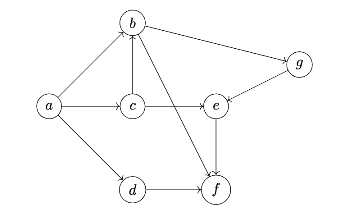
What will be the finish time of node \(c\)? Assume the convention that a node's neighbors are produced in alphabetical order.
Problem #250
Tags: breadth first search
Suppose a connected, undirected graph \(G\) has \(n\) nodes, half of which are ``red'' and half of which are ``blue''. Each red node shares an edge with \(\log_2 n\) blue nodes, and the only edges in the graph are between red and blue nodes.
What is the time complexity of BFS when run on \(G\)? Your answer should be in asymptotic notation and in terms of \(n\), in as simplest terms possible.
Problem #251
Tags: breadth first search
The code below is a modified version of BFS shown in class. This modification has a single addition: a print statement. A comment in the code indicates where the print statement is located.
def bfs(graph, source):
"""Start a BFS at `source`."""
status = {node: 'undiscovered' for node in graph.nodes}
status[source] = 'pending'
pending = deque([source])
while pending:
u = pending.popleft()
for v in graph.neighbors(u):
print("here!") # <--- this is the print statement
if status[v] == 'undiscovered':
status[v] = 'pending'
pending.append(v)
status[u] = 'visited'
Suppose this modified BFS is run on the following graph, starting at node \(a\).
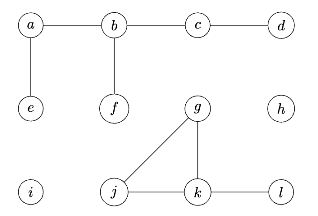
How many times will "here!" be printed? Your answer should be an exact number.
Problem #252
Tags: start and finish times
Let \(G\) be an undirected graph, and let \(u\) and \(v\) be two nodes in the graph, with \(v\) reachable from \(u\).
Suppose that at the moment dfs(u) is called, \(v\) is still undiscovered. True or False: the eventual start time of \(v\) must be less than the finish time of \(u\).
Solution
False